Lekcja 8. Sortowanie¶
Sortowanie to jeden z najbardziej podstawowych problemów informatyki. Polega on na uporządkowaniu pewnego zbioru danych zgodnie z pewnym kryterium. Kryterium tym najczęściej są wartości elementów, np. sortowanie liczb w porządku rosnącym, sortowanie słów alfabetycznie itp.
Sortowanie jest konieczne nie tylko dla wygodniejszej percepcji danych przez użytkownika, ale przede wszystkim w celu wydajniejszego stosowania innych procedur. Dobrym przykładem jest, poznany na poprzedniej lekcji, algorytm przeszukiwania binarnego, który wymaga posortowanego zbioru danych do działania.
Najważnieszymi parametrami, jakimi charakteryzuje się algorytmy sortowania (podobnie jak wszystkie inne), są złożoność algorytmiczna oraz wymagania pamięciowe. Algorytmy sortowania, które wymagają dodatkowej pamięci, nazywają się algorytmami zewnętrznymi. Algorytmy, które nie potrzebują większej niż pewna stała ilość pamięci (sortowane dane są przez cały czas przechowywane w tej samej strukturze, np. tablicy) są nazywane algorytmami sortowania w miejscu.
Drugim ważnym parametrem jest złożoność algorytmiczna. Nie wdając się w dłuższe wywody możemy tylko wspomnieć, że algorytmy pesymistyczne mają złożoność \(O(n^2)\), algorytmy z dobrą złożonością wykonują się w czasie \(O(n\cdot \log n)\) a idealne mają złożoność \(O(n)\) (mówimy, że wykonują się w czasie liniowym).
Zapoznajmy się bliżej z podstawowymi algorytmami sortowania.
Sortowanie bąbelkowe¶
Sortowanie bąbelkowe (ang. “bubble sort”) to prosty algorytm polegający na porównywaniu elementów parami. Jeśli kolejność jest zaburzona (element większy jest przed mniejszym), to są one zamieniane ze sobą miejscami. Po dojściu do końca algorytm powraca do początku i procedura jest powtarzana. Algorytm kończy działanie, jeśli podczas przejścia nie dokonał żadnych zmian. Prześledźmy to na prostym przykładzie:
Mamy tablicę \([6,3,1,2,5,4]\), każda linijka poniżej opisuje jeden przebieg, podkreślenie oznacza elementy, które są porównywane:
Zastanówny się, jakie są wymagania tego algorytmu. Dla tablicy o długości \(n\) w każdym przebiegu musimy wykonać \(n-1\) porównań. Do tego w pesymistycznym wariancie [1] należy wykonać \(n\) przebiegów, dlatego całkowita złożoność algorytmu wynosi \(O(n^2)\). Jednocześnie wszystkie operacje wykonujemy na tej samej tablicy, dalego jest to algorytm pracujący w miescu (wymagania pamięciowe wynoszą \(O(1)\).
Jak widać, przebieg algorytmu powoduje “wypchnięcie” największego elementu na koniec. Dlatego możemy ulepszyć algorytm, po każdym przebiegu skracjąc przeszukiwanie o ostatnią pozycję. Ostateczny algorytm ma postać:
bubble(A):
n = len(A)-2
dopóki n > 1:
dla i od 0 do n:
jeżeli A[i] > A[i+1]:
zamień miejscami A[i] i A[i+1]
n = n - 1
zwróć A
Zadanie 8.1
Powyższy algorytm ma jedną wadę: jeśli w trakcie \(k\)-tego przebiegu (\(k<n-1\)) tablica będzie posortowana, to algorytm będzie działał dalej. Zmodyfikuj go zgodnie z pierwotnym założeniem, to znaczy żeby przerywał działanie, jeśli podczas przebiegu nie została wykonana żadna zamiana.
Aby za każdym razem nie wpisywać tablicy do posortowania, możemy skorzystać z poniższego kodu:
Zadanie 8.2
Napisz progtam implementujący powyższy algorytm. Do generowania losowej listy do posortowania możesz wykorzytać powyższy kod.
Na koniec - demonstracja sortowania bąbelkowego przy pomocy... tańca ludowego:
| [1] | Zastanów się, jaki wariant wstępnego ułożenia tablicy jest najbardziej pesymistyczny, to znaczy będzie wymagał najwięcej powtórzeń. |
Sortowanie przez scalanie¶
Innym algorytmem sortowania jest “Sortowanie przez scalanie” (ang. “Merge sort”). Jest to sztandarowy przykład algorytmu “dziel i zwyciężaj”, szczegółowo omawianego na poprzedniej lekcji:
- Jeśli lista jest jednoelementowa, to z definicji jest posortowana
- Jeśli lista jest dłuższa, to ją podziel na (nierówne w przypadku nieparzystej liczby elementów) połowy.
- Posortowane podlisty scal w posortowaną listę.
Pierwszy punkt nie wymaga komentarza. Drugi również jest dość oczywisty. Rekurencyjnie dzielimy listę na pół tak długo, aż będziemy mieć \(n\) list o długości \(1\).
Schemat podziału jest przedstawiony na rysunku:
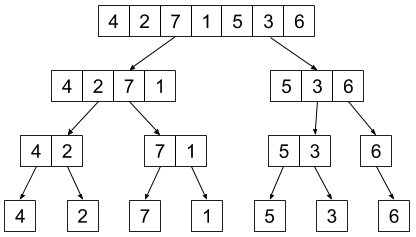
Kiedy już mamy \(n\) list jednoelementowych, możemy je scalić zgodnie z poniższym rysunkiem:
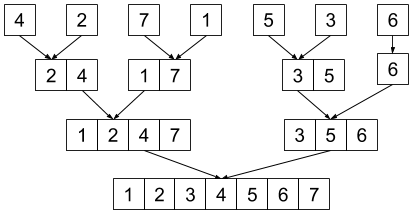
Scalanie dwóch list jest przeprowadzane w następujący sposób: bierzemy najmniejszy element z każdej listy i porównujemy ze sobą, mniejszy z nich usuwamy i wwstawiamy na początku nowej listy. Czynności powtarzamy tak długo, aż obie listy będą puste. Procedurę tę ilustruje poniższy rysunek:
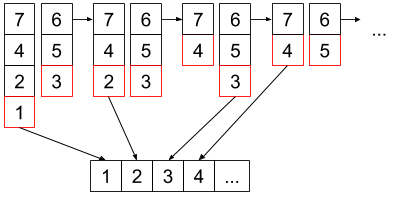
Znamy już wszystkie elementy składowe, więc możemy zapisać pełen algorytm:
msort(lista):
jeżeli dlugosc_listy < 2: # lista jednoelementowa
zwróć lista
srodek = n/2
lewa = msort(lewa polowa listy)
prawa = msort(prawa polowa listy)
dopóki dlugosc_lewej > 0 i dlugosc_prawej > 0:
jeżeli lewa[0] < prawa[0]:
wynik += lewa[0]
usun lewa[0]
w przeciwnym wypadku:
wynik += prawa[0]
usun prawa[0]
wynik += lewa
wynik += prawa
zwroc wynik
Zaimplementujmy powyższy algorytm:
Zadanie 8.3
Wyjaśnij, do czego służą Instrukcje w liniach \(13\) i \(14\). Podpowiedź: zwróć uwagę na warunek pętli while.
Powyższy kod ma poważny mankament związany z wydajnością. Otóż usuwanie pierwszego elementu listy powoduje przeindeksowanie całej listy, co jest operacją o koszcie \(O(n)\). Dlatego lepiej jest użyć pomocniczych liczników indeksujących listy “lewa” i “prawa” i przesuwać indeksy zamiast usuwać elementy list. Po drugie – nie musimy używać pomocniczej listy “wynik” – po utworzeniu list “lewa” i “prawa” oryginalna lista nie jest już potrzebna, więc możemy użyć jej jako wynikowej.
Zadanie 8.4
Zmodyfikuj program uwzględniając powyższe uwagi. Porównaj na przykładowych zestawach danych, na ile szybciej działa program po poprawkach.
Na koniec wspomnijmy o wydajności algorytmu sortowania przez wstawianie. Algorytm ten należy do algorytmów zewnętrznych (wymaga dodatkowej pamięci na przechowywanie tymczasowych list) a jego złożoność algorytmiczna wynosi \(O(n\cdot\log n)\). Bliżej zainteresowanych tematem odsyłamy do literatury [2] [3]
Ponownie, jak w przypadku sortowania bąbelkowego, taneczna demonstracja alorytmu:
| [2] | Cormen Thomas H., Leiserson Charles E., Rivest Ronald L, Clifford Stein, Wprowadzenie do algorytmów, PWN Warszawa 2013, ISBN 9788301169114 |
| [3] | https://en.wikipedia.org/wiki/Merge_sort |
Sortowanie szybkie¶
Sortowanie szybkie (ang. “quicksort) również jest algorytmem typu “dziel i zwyciężaj”. Jego zaletą, w porówaniu do sortowania przez scalanie, jest brak wymogu dodatkowej pamięci. Minusem jest fakt, że sortowana struktura nie jest dzielona na równe połowy, co w pewnych szczególnych przypadkach może prowadzić do obniżenia wydajności. W ogólności jednak algorytm sortowania szybkiego jest na tyle wydajny, że jest powszechnie używany i większość języków programowania ma jego implementację w standardowych bibliotekach. Przyjrzyjmy się bliżej zasadzie jego działania.
W algortmie wybieramy jedną wartość, nazywaną “wartością rozdzielającą” (ang. “pivot value”). Algorytm przeszukuje tablicę i wszystkie elementy mniejsze (a dokładniej mówiąc – nie większe) od wartości rozdzielającej umieszcza po jej lewej stronie; elementy większe od wartości rozdzielającej umieszczane są po jej prawej stronie. Następnie tablica jest dzielona na pozycji wartości rozdielającej (punkt podziału, splitpoint) na dwie i procedura (nazywana partycjonowaniem, partitioning) jest rekurencyjnie powtarzana aż do uzyskania tablic jednoelementowych (które, jak wiemy, są z definicji posortowane).
Procedurę przedstawiono na rysunku. Zaczynamy od nieposortowanej listy, wybieramy wartość rozdzielającą (\(4\), oznaczona na czerwono). Wybieramy również dwa markery “L” i “R” wskazujące na lewy i prawy koniec analizowanej tablicy.
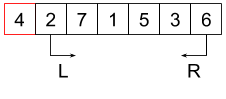
Jeżeli wartość pod markerem “L” jest nie większa od rozdzielającej to przesuwamy marker o jedną pozycję w prawo. Analogicznie jeśli wartość pod markerem “R” jest większa od wartości rozdzielającej, to przesuwamy marker o jedną pozycję w lewo. Robimy to tak długo, aż natrafimy na wartości “nie na swoim miejscu” (większą od pivota pod lewym markerem albo mniejszą pod prawym).
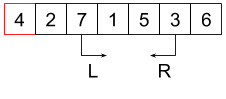
W momencie, gdy oba markery się zatrzymały, możemy wartości pod nimi zamienić miejscami i kontynuować. Cała procedura kończy się w momencie, gdy markery się skrzyżują (to znaczy lewy marker znajedzie się na prawo od prawego. Wtedy zamieniamy ze sobą wartość spod prawego markera i wartość rozdzielającą. Osiągnęliśmy cel - elementy po lewej od pivota są od niego nie większe, a te po prawej - większe. Możemy więc rodzielić listę na pozycji pivota. Wybieramy dla każdej z nich mową wartość rozdzielającą i rekurencyjnie powtarzamy procedurę.
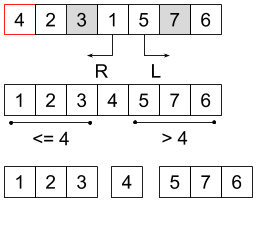
Gotowy program wykorzystujący algorytm sortowania szybkiego przedstawia poniższy kod:
Powyższy program jako wartość rozdzielającą zawsze bierze pierwszy element listy. Wybór “pivota” jest bardzo ważny i wpływa na szybkość wykonywania algorytmu. Przypadek optymistyczny (najlepszy) to taki, gdy jako pivot zawsze wybierzemy medianę (wartość leżącą pośrodku, to znaczy większą i mniejszą od dokładnie połowy wszystkich). Z drugiej strony przypadek pesymistyczny (najgorszy) to taki, gdy jako pivot za każdym razem wybierzemy wartość skrajną. Dlatego wybór pierwszego elementu nie jest najszczęśliwszy, jeśli spróbujemy posortować listę już posortowaną, to taki przypadek okaże się paradoksalnie najgorszym możliwym! Jedną ze strategii radzenia sobie z tym problemem jest wybór pivota jako “mediany z trzech”:
- Wybieramy pierwszy, środkowy i ostatni element z listy.
- Porównujemy ich wartości.
- Środkowy z nich wybieramy jako pivot.
Zadanie 8.5
Zmodyfikuj program, aby jako wartość rozdzielającą wybierał “medianę z trzech”. Porównaj szybkość działania obu programów na następujących listach:
- Losowej (nieposortowanej)
- Posortowanej
- Posortowanej odwrotnie (malejąco).
Jakie wnioski możesz wysnuć?
Na koniec podrozdziału oczywiście taniec. Tym razem algorytm lekko zmodyfikowany, czy rozpoznajesz różnice między algorytmem odtańczonym, a omawianym w lekcji?
Inne algorytmy sortowania¶
Niniejszy przegląd nie stanowi oczywiście pełnego ujęcia tematu. Nie wspomnieliśmy o wielu interesujących algortymach sortowania, jak na przykład “heapsort” (“sortowanie przez kopcowanie”), “Radix sort” (“sortowanie pozycyjne”) czy sortowaniu przez wstawianie (“insert sort”). Osoby zainteresowane tematem gorąco zachęcamy do zapoznania się z literaturą przedmiotu (np. wcześniej wspomniany podręcznik Cormena), a na zachętę – jeszcze jeden film, tym razem bez tańca.