Lekcja 7. Algorytm “Dziel i zwyciężaj”¶

Przykładowy problem: porządkowanie talii kart¶

Problem: cztery osoby grały w “Makao” używając dwóch talii kart, z czerwonymi i niebieskimi koszulkami. Po skończonej grze trzeba karty schować - do jednego pudełka czerwone, do drugiego niebieskie.

Algorytm naiwny w tym przypadku wygląda następująco:

While(na stosie są karty):
  weź_kartę
  if karta = czerwona:
    połóź_po_prawej
  else:
    połóź_po_lewej

Ale w grupie mamy czwórkę graczy! Więc możemy:

1. podzielić karty na cztery kupki i dać po jednej każdemu z graczy
2. każdy gracz dzieli swoją część
3. posortowane kupki składamy razem: lewe do jednego pudełka, prawe - do drugiego

W ogólnym (chociaż mało realistycznym) przypadku, jeśli mamy nieskończoną [1] liczbę graczy, to każdy dostaje tylko jedną kartę i od razu wkłada ją do właściwego pudełka. W tym wypadku podproblem okazuje się trywialny i “sam” się rozwiązuje.

Wieża Hanoi¶

Zastanówmy się nad innym problemem, który można rozwiązać programistycznie.

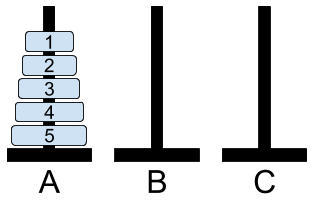
Rozpatrzmy klasyczną grę jednoosobową Wieże Hanoi. Gra polega na tym, że mamy planszę z trzema słupkami, oznaczonymi literami “A”, “B” i “C”, oraz \(n\) krążków o różnej średnicy zewnętrznej. Krążki są nawleczone w piramidę (największy na dole, na nim coraz mniejsze) na słupku “A”. Należy przenieść je na słupek “B” zachowując następujące reguły:

1. W każdym ruchu wolno przenieść tylko jeden krążek.
2. Nie wolno kłaść krążka większego na mniejszym.
3. Wolno korzystać z pomocniczego słupka “C”.

Zastosujmy podejście “Dziel i zwyciężaj”:

1. Jeżeli na słupku “A” mamy tylko jeden krążek (\(n=1\)), to możemy go przełożyć na słupek “B” - zadanie rozwiązane!
2. Jeżeli \(n>1\), to przenieśmy piramidę \(n-1\) krążków ze słupka “A” na słupek “C” (korzystając z “B” jako pomocniczego).
3. Przenieśmy ostatni \(n\)-ty krążek na słupek “B”.
4. Przenieśmy piramidę \(n-1\) krążków ze słupka “C” na “B” korzystając z “A” jako pomocniczego.

Zauważ, że pierwsze dwa kroki możemy połączyć w jeden, zmieniając warunek na \(n>0\) (zastanów się, dlaczego).

Zapiszmy powyższy przepis w pseudokodzie:

Hanoi(n, źródło, cel, pomocniczy):
  jeżeli n > 0:
    Hanoi(n-1, źródło, pomocniczy, cel)
    przenieś(źródło, cel)
    Hanoi(n-1, pomocniczy, cel, źródło)

Możemy teraz napisać program. Nie będziemy go zbytnio komplikować grafiką, więc przedstawimy słupki w postaci list a rozmiary krążków w postaci liczb.

Wyszukiwanie binarne¶

Kolejnym, bardzo ważnym i jednocześnie stosunkowo łatwym do zrozumienia problemem jest wyszukiwanie binarne. Załóżmy, że szukamy konkretnej wartości \(T\) w tablicy \(A=[a_0, a_1, a_2, \ldots, a_{n-1}]\). Tablica \(A\) jest posortowana niemalejąco, tzn. \(a_0\le a_1\le\ldots a_{n-1}\)

Można zastosować poznaną na poprzedniej lekcji metodę siłową: porównywać po kolei wszystkie elementy tablicy z poszukiwaną wartością. Łatwo pokazać, że koszt algorytmiczny takiego podejścia wynosi \(O(n)\), to znaczy algorytm ma liniową złożoność.

Możemy jednak zastosować podejście “Dziel i zwyciężaj” dzieląc tablicę na pół i przeszukując tylko jedną połowę. Wyboru połowy dokonujemy na podstawie środkowej wartości. W poprzednim przykładzie skupialiśmy się na algorytmie rekurencyjnym, więc dla odmiany zapiszmy algorytm iteracyjny:

lewy = 0
prawy = n - 1
dopóki lewy <= prawy i nie znaleziono K:
  srodek = (lewy + prawy) // 2
  jeżeli A[srodek] = K:
    znaleziono K
  w przeciwnym wypadku:
    jeżeli A[srodek] > K:
      prawy = srodek - 1
    w przeciwnym wypadku:
      lewy = srodek + 1

Prześledźmy działanie algorytmu na przykładzie: \(A = [1, 5, 9, 18, 22, 34, 94, 135, 181], K = 18\):

1. Zaczynamy od wyznaczenia środka, \(srodek = (0+8)//2=4\)
2. Ponieważ \(A[4] = 22 > 18\), to \(prawy = 4 - 1 = 3, srodek = (0 + 3)//2 = 1\)
3. \(A[1] = 5 < 18, lewy = 1 + 1 = 2, srodek = (2 + 3) //2 = 2\)
4. \(A[2] = 9 < 18, lewy = 2 + 1 = 3, srodek = (3 + 3) //2 = 3\)
5. \(A[3] = 18 = 18\), znaleziono K

Zapiszmy powyższy algorytm w postaci programu:

Przeanalizuj kod dla różnych wartości. Co się dzieje, jeśli wartość szukana jest mniejsza niż pierwszy lub większa niż ostatni element listy?

Metoda równego podziału¶

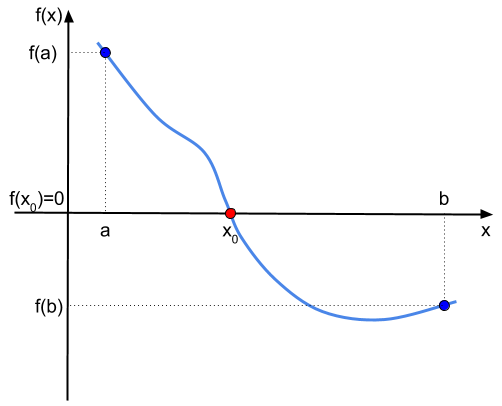
Kolejny problem należy do metod numerycznych - przybliżonych metod obliczeń matematycznych. Mamy funkcję ciągłą, zdefiniowaną na domkniętym przedziale \([a,b]\). Dodatkowo funkcja ma przeciwne znaki na końcach tego przedziału. Wiadomo więc, że w tym przedziale występuje miejsce zerowe (a dokładniej nieparzysta liczba miejsc zerowych) tak, jak to pokazano na rysunku:

Algorytm poszukiwania miejsca zerowego jest bardzo podobny do algorytmu wyszukiwania binarnego:

dopóki f(m) jest różne od 0:
  znajdź środek m przedziału [a, b]
  wybierz tę połowę, w której funkcja na końcach ma przeciwne znaki

Tutaj napotykamy na problem – program napisany na podstawie tego algorytmu będzie prawdopodobnie działał w nieskończoność (a przynajmniej bardzo długo).

Jest to związane z tym, że metoda bisekcji (metoda równego podzialu) jest metodą przybliżoną: obliczane w kolejnych krokach wartości funkcji będą się zbliżać do zera, ale nie muszą go osiągnąć.

Dlatego należy wprowadzić dodatkowe założenie - dokładność, przy jakiej chcemy przerwać obliczenia. Można to zrobić na trzy sposoby:

1. Przerwać, kiedy szerokość przedziału jest mniejsza niż zadana wartość \(b - a < \varepsilon\)
2. Przerwać po zadanej liczbie kroków (powtórzeń pętli)
3. Przewać, gdy wartość funkcji (a dokładniej jej moduł, czyli wartość bezwględna) będzie mniejsza od zadanej wartości \(|f(m)| < \varepsilon\)

Ostatnim brakującym elementem jest warunek przeciwnych znaków. Możemy go łatwo sprawdzać, mnożąć wartości funkcji przez siebie. Jeśli wynik jest ujemny, to mnożone liczby mają przeciwne znaki.

Zapiszmy więc ostateczny algorytm:

dopóki (b - a) > eps:
  m = (a + b) / 2.0
  jeżeli f(m) = 0:
    zwróć m
  w przeciwnym przypadku:
    jeżeli f(a) * f(m) < 0:
      b = m
    w przeciwnym przypadku:
      a = m

zwróć m

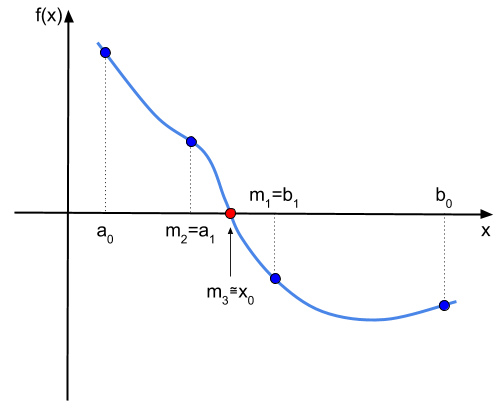
Działanie tego algorytmu zostało przedstawione na rysunku: