Lekcja 2. Sterowanie pracą programu.¶
Na poprzednich zajęciach poznaliśmy logiczny typ danych bool. Literały
tego typu mogą przyjmować jedną z dokładnie dwóch wartości: True (prawda)
bądź False (fałsz). W wielu językach programowania przyjęto liczbę 0
jako odpowiednik fałszu i 1 (lub w ogólności każdą inną liczbę) jako
odpowiednik prawdy. Można też spotkać się z nazwą typu boolean (np. w
bardzo popularnym języku Java). Dla typu logicznego mamy w języku Python
zdefiniowane operatory standardowe. Tutaj ciekawostka - typ bool pojawił
się w języku Python dopiero w wersj 2.3, a powodem tego była troska o
czytelność kodu.
Nazwa typu logicznego to oczywiście jednocześnie nazwa funkcji bool(obj),
która powoduje rzutowanie zmiennej właśnie na typ logiczny
Przypomnimy sobie krótko operatory logiczne. Z poprzedniej lekcji wiemy, że
podstawowe operatory logiczne to and (logiczne i), or (logiczne lub)
oraz not (logiczna negacja). Znajdziecie też tam omównienie operatorów
porównania (<, ==...), w wyniku działania których również dostajemy
literały typu bool. Ten właśnie typ jest podstawą do konstrukcji
rozgałęzień programów. Rozgałęzienie to takie miejsce w programie
komputerowym, w którym na podstawie jakiegoś zdania logicznego decydujemy co
program ma dalej wykonywać. W najprostszym przypadku program rozdziela się na
dwie części.
Rozgałęzienia¶
W języku Python instrukcją rozgałęziającą program jest if, co tłumaczymy
jako ‘jeżeli’. Gdybyśmy chcieli postawić problem
jeżeli zmiennaxjest mniejsza od liczby0to zmień ją na liczbę nieujemną, a w przeciwnym przypadku nie rób nic
dostajemy właśnie takie rozgałęzienie. Formalnie możemy zapisać to w postaci kodu:
if x < 0: x = -x
Aby zobrazować to rozgałęzienie, możemy też użyć schematu blokowego. Jest to jedna z możliwości przedstawienia danego problemu (później będziemy używać słowa algorytm).
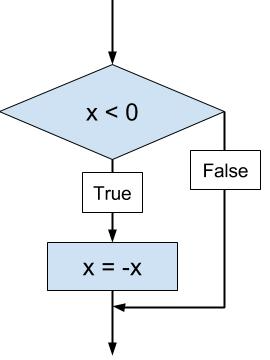
Rozgałęzienie - schemat blokowy.
Ogólny schemat rozgałęzienia w języku Python ma postać:
if WARUNEK:
BLOK_INSTRUKCJI_IF
elif WARUNEK_1:
BLOK_1
elif WARUNEK_2:
BLOK_2
...
else:
BLOK_ELSE
Widzimy dwie nowe instrukcje: elif oraz else. Pierwszą moża odczytać
jako else if i należy rozumieć w przypadku gdy. Ostatnią instrukcją jest
else, która oznacza w każdym innym przypadku. Obowiązkową konstrukcją
jest zastosowanie słowa kluczowego if, wszystkie inne słowa są opcjonalne.
Służą one nieco bardziej skomplikowanym rozgałęzieniom. Python będzie
sprawdzał powyższe warunki po kolei, jeden po drugim. Jeżeli napotka na
warunek który będzie prawdą, to reszta warunków nie będzie już sprawdzana.
Co więcej - bloki instrukcji nie będą nawet interpretowane. Sprawdzana będzie
tylko poprawność składni.
Popatrzmy na przykład. Przetestujemy, czy zmienna liczba wskazuje na
liczbę parzystą.
Oczywiście w powyższym przykładzie zobaczymy, że ‘liczba jest parzysta’. Pobaw
się powyższym kodem, zobacz, dla jakich liczb otrzymujemy informację o
liczbach parzystych, a dla jakich nie. Zobaczymy, jak wygląda nieco bardziej
skomplikowany przykład rozgałęzień. Parzystość liczby oznacza, że jest ona
podzielna przez 2 bez reszty. Ale jak sprawdzić, czy liczba jest podzielna
przez 2 oraz przez 3 jednocześnie? Jeżeli powiemy, że rozgałęzienia można
zagnieżdżać, tzn: czyli kolejne rozgałęzienia (konstrukcje if - elif - ... -
else), można umieszczać w odpowiednich blokach rozgałęzień to konstrukcja
stanie się bardzo podobna do powyższej.
Zmieniając zmienne A i B możecie posprawdzać, czy wybrana liczba
jest podzielna przez dowolną parę innych liczb.
Zadanie 2.1
Powyższy program ma pewną słabość i nie zawsze będzie kończył się bez błędu. Postaraj się wygenerować błąd, a potem go naprawić.
Na koniec tego podrozdziału omówimy wybór największej z trzech liczb.
W tym miejscu warto zaznaczyć, że w języku Python nie znajdziemy instrukcji
wyboru (podobnej do switch z C). Taką instrukcję można oczywiście łatwo
zasymulować powyższą konstrukcją if - elif - else.
Zadanie 2.2
Na koniec proste zadanie. Napisz program sprawdzający, która z 3 podanych
liczb U, V, W jest największą liczbą parzystą. Jeżeli wśród podanych
liczb parzystej nie ma, to program powinien o tym fakcie informować.
Pętle w języku Python¶
Najbardziej uniwersalną konstrukcją języka Python, umożliwającą wykonywanie
bloku instrukcji wielokrotnie jest instrukcja while. Podobnie jak
rozgałęzienie bazuje ona na warunku logicznym.
while WARUNEK:
BLOK_WHILE
Tak długo jak długo spełniony jest warunek (zwraca True), tak długo
wykonywany będzie blok instrukcji BLOK_WHILE. Aby zwrócić kwadraty liczby
od 1 do 5, musimy napisać:
Ostatnia linia (numer 5) jest bardzo istotna. Jeżeli jej zapomnimy, co zdarza
się nadspodziewanie często, pętla wykonywać się będzie w nieskończoność.
Poniżej znajdziecie tabelę, w której podane są, krok po kroku, wszystkie
wartości zmiennej num i jej kwadratu, a także wynik testu num >= 5.
Proszę zauważyć, że zmienna kwadrat_num nie zostanie obliczona dla num =
6.
| num | kwadrat_num | num <= 5 |
|---|---|---|
| 1 | 1 | True |
| 2 | 4 | True |
| 3 | 9 | True |
| 4 | 16 | True |
| 5 | 25 | True |
| 6 | False |
Znając już dwie konstrukcje warunkowe if oraz while, możemy już
konstruować dowolnie skomplikowane problemy. W zasadzie możemy rozwiązać
dowolne zadanie programistyczne. Nie zawsze będzie to łatwe, ale da się to
zrobić. Spróbujemy wypisać teraz liczby podzielne przez 2 i 3 większe od 33 i
mniejsze od 67.
Zadanie 2.3
Napisz program obliczający sumę wszystkich liczb parzystych podzielnych
przez A i B, w granicy od START do STOP. Dla liczb A =
6 oraz B = 5 oraz START = -101 oraz STOP = 1303 powinieneś
dostać wartość 28200. Możesz oczywiście zmodyfikować powyższy
ActiveCode 6.
Na koniec tego podrozdziału dodamy, że podobnie jak dla rozgałęzień pętlę
while możemy napisać z wykorzystaniem słowa else. Konstrukcja będzie
następująca:
while WARUNEK:
BLOK_WHILE
else:
BLOK_ELSE
i rozumieć możemy ją dokładnie tak jak znaną już konstrukcję if - else. W
momencie, gdy WARUNEK nie będzie spełniony, uruchomi się blok instrukcji
przy else. Mamy dwie takie możliwości:
pętla
whilewykona się do końca i po niej wywoła się blokelsei = 1 while i < 2 ** 3: print 2 ** i i += 1 else: print 'koniec dzialania petli'
pętla
whilenie wykona się w ogóle (warunek nie będzie spełniony), wykona się natomiast blokelsei = 100 while i < 2 ** 3: print 2 ** i i += 1 else: print 'petla while nie wywola sie wcale'
W języku Python znajdziemy jeszcze jeden, bardzo użyteczny rodzaj pętli, pętlę
for. Wykorzystuje ona do działania typy sekwencyjne, czyli takie, które
posiadają elementy, kóre można odliczać. Zanim omówimy składnię for
musimy te typy poznać.
Typy sekwencyjne¶
Do typów sekwencyjnych zaliczymy listy (list), krotki (tuple),
łańcuchy znaków (str). Innym typem zmiennych po których można iterować,
ale nie zaliczamy ich do sekwencji, są słowniki (dict).
Łańcuchy znaków¶
Tak naprawdę poznaliśmy już jeden taki typ - jest to łańcuch (ciąg) znaków,
czyli typ str. Na łańcuch 'Mielonka i jajka' możemy spojrzeć jak na
zbiór znaków, gdzie pierwszym znakiem jest M, drugim i, trzecim e
i tak dalej. Możemy więc ponumerować znaki w takim łańcuchu. W języku Python
przyjęło się numerować od liczby 0, zatem ostatnim znakiem jest zawsze
liczba długość_ciągu_znaków - 1. W przypadku naszego ciągu literze M
odpowiadać będzie liczba 0, literze i liczba 1, e - 2,
itd. Owe liczby (0, 1, 2...) nazywamy indeksami. Służyć będą one do
odwołania się do konkretnego miejsca w łańcuchu. Odwołanie takie wykonuje się
za pomocą nawiasów kwadratowych:
ciag_znakow[indeks]
Na bazie powyższego łańcucha znaków odwołamy się do indeksów 2 i 4,
czyli odpowiednio do trzeciego i czwartego miejsca w łańcuchu. Zobaczmy, jak
to działa w ActiveCode
Ostatnim indeksem w zmiennej tekst jest liczba 15. Jest to liczba równa
długość_ciągu_znaków - 1. Aby obliczyć długość sekwencji możemy posłuzyć
się funkcją len(seq), co oznacza, że ostatni dostępny indeks sekwencji
seq dany jest wzorem len(seq) - 1 i właśnie za pomocą takiego
wyrażenia możemy odwołać się do ostatniego elementu sekwencji.
seq[len(seq) - 1]
Drugim od końca elementem będzie oczywiście seq[len(seq) - 2] itd.
Wypisywanie (i obliczanie) za każdym razem długości sekwencji nie jest
szczególnie korzystne i Python umożliwia nam odwoływanie się do sekwencji od
końca po prostu za pomocą ujemnych indeksów.
Poniższa tabela podsumowuje możliwości odwoływań do poszczególnych miejsc w
sekwencji s = "Python".
| P | y | t | h | o | n |
|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 |
| len(s) - len(s) | len(s) - 5 | len(s) - 4 | len(s) - 3 | len(s) - 2 | len(s) - 1 |
| -len(s) | -5 | -4 | -3 | -2 | -1 |
Wycinanie sekwencji¶
Za pomocą indeksów możemy też odwołać się do większej części sekwencji. Służy do tego technika wycinania sekwencji (sequence slicing). Ogólna postać wycinania wygląda następująco:
seq[start:stop:krok]
Jak widać musimy w ogólności podać 3 liczby:
start- indeks, od którego mamy zacząć wycinaćstop- indeks, na którym wcięcie ma się zakończyć, wartość stojąca pod tym indeksem jest pomijanakrok- co który indeks ma być brany pod uwagę przy wycinaniu
Zerknijmy na prosty przykład. Proszę zauważyć, że do argumnetów start,
stop i krok możemy podstawiać liczby zarówno dodatnie, jak i ujemne.
Zero oczywiście też.
Specjalnego typu krokiem jest 1. Jeżeli krok = 1 oznacza to, że mamy
na myśli każdy indeks z żądanego zakresu. Jedynka jest wartością domyślną w
tego typu iteracjach i możemy ją pominąć.
>>> tekst[2:5] == tekst[2:5:1]
True
Specjalnymi indeksami są 0 oraz -1 (len(seq) - 1). Oznaczają one
początek i koniec sekwencji. Miejsca te są dla interpretera oczywiste, dlatego
i je możemy pomijać, wycinając sekwencje.
Podobne odwołania można wykonywać na sekwencjach dowolnego typu.
Operatory zawierania elementu w sekwencji¶
Dla sekwencji istnieją specjalne operatory zawierania się danego elementu w
zbiorze, sekwencji. Operator in testuje obecność elementu w zbiorze, a
operator not in sprawdza, czy elementu nie ma.
>>> seq = 'Mielonka i jaja'
>>> 'M' in seq
True
>>> 'z' not in seq
True
Jak widać wynik działania tych operatorów jest typu bool.
Listy¶
Lista jest najbardziej ogólnym rodzajem sekwencji. Podobnie jak typ str
obiekty tego typu to uporządkowane sekwencje, nie mają jednak ustalonej
wielkości, są to zatem obiekty modyfikowalne (zmienne). Operacje na nich
są podobne do tych, które możemy wykonywać na łańcuchach (możemy je wycinać,
odwoływać się po indeksach, sprawdzać ich długość). Zmienną o typie list
tworzymy tradycyjnie za pomocą nazwy oraz operatora przypisania. Aby
zaznaczyć, że budujemy właśnie listę posługujemy się nawiasami kwadratowymi
[]
L1 = [1, 2, 3]
L2 = []
Pierwszy obiekt o nazwie L1 będzie listą o 3 elementach, drugi L2
będzie pustą listą (listą nieposiadającą żadnych elementów). W związku z tym
długość tej pierwszej to właśnie 3 a drugiej 0 (sprawdź to!).
Listy można łączyć za pomocą operatora +, zupełnie jak łańcuchy znaków.
Pisząc L1 + L2 tworzymy po prostu nowy obiekt, który będzie listą powstałą
ze sklejenia list L1 i L2. Listy możemy natomiast modyfikować, czego
nie można powiedzieć ani o łańcuchach, ani o krotkach. O tych drugich za
chwilę, a na razie zerknijmy na możliwości modyfikacji. Najprostszą
modyfikacją jest zmiana konkretnego elementu za pomocą odwołania poprzez
indeks.
Jak widać elementy list nie muszą być tego samego typu. Ma to swoje plusy i minusy - z jednej strony nie musimy się gimnastykować, żeby w jednej strukturze przechować informacje o różnych typach, z drugiej tzreba być uważnym programistą, aby nie próbować za chwilę takiej wysumować elementów takiej listy.
Modyfikacje i inne operacje specyficzne dla list¶
Wspominaliśmy na początku tego podręcznika, że język Python jest językiem obiektowym. Pewną operacją typową dla obiektów jest odwoływanie się do zaszytych w nich parametrów i funkcji poprzez tak zwane odwołanie przez kropkę. Nie chcemy w tym momencie wchodzić głębiej w idee Programowania Zorientowanego Obiektowo (PZO), będziemy jeszcze do tego wracać w dalszej części podręcznika. Na razie najlepiej zapamiętać składnię takiego odwołania:
# odwolanie do funkcji (metody)
obiekt.funkcja(argumenty)
# oraz zmiennej (pola)
obiekt.zmienna
Funkcję specyficzną dla danego obiektu nazywamy metodą, choć póki co nie
ma co sobie zaprzątać takim nazwenictwem głowy. Listy mają takich metod kilka.
Załóżmy, że mamy do dyspozycji listę L
L.append(obj): dodaje element na koniec listyLL.extend(innaL): rozszerza listę poprzez dołączenie wszystkich elementów podanej listynowaLL.insert(idx, obj): wstawia elementobjna podaną pozycję listyidxL.remove(obj): usuwa pierwszy napotkany elementobjz listy; jeżeli nie ma na liście takiego elementu, zgłaszany jest błądL.pop([idx]): usuwa element z podanej pozycjiidxna liście i zwraca go jako wynik; jeżeli nie podano żadnego indeksu a.pop(), usuwa i zwraca ostatni element z listyL.index(obj): zwraca indeks pierwszego elementuobjlistyL.count(obj): zwraca liczbę wystąpień elementuobjw liścieL.sort(): sortuje elementy listy w niej samej; jest to operacja nieodwracalnie modyfikująca listęLL.reverse(): odwraca kolejność elementów listy w niej samej
Wypróbujemy kilka z nich: Stworzymy listę L, dodamy do niej kwadraty liczb od 1 do 10. Następnie usuniemy i dodamy różnymi metodami kilka liczb.
Listy można w sobie zagnieżdżać, czyli tworzyć listy list. Taką listę możemy stworzyć odpowiednio ją inicjalizując lub też dynamicznie:
Zadanie
Za pomocą pętli while zbuduj listę tabliczka, reprezenującą tabliczkę
mnożenia. Użyj liczb odpowiadających indeksom, od 0 do 10 włącznie. Wynik
powinien wyglądać m/w tak:
print tabliczka
[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[2, 4, 6, 8, 10, 12, 14, 16, 18, 20],
[3, 6, 9, 12, 15, 18, 21, 24, 27, 30],
[4, 8, 12, 16, 20, 24, 28, 32, 36, 40],
[5, 10, 15, 20, 25, 30, 35, 40, 45, 50],
[6, 12, 18, 24, 30, 36, 42, 48, 54, 60],
[7, 14, 21, 28, 35, 42, 49, 56, 63, 70],
[8, 16, 24, 32, 40, 48, 56, 64, 72, 80],
[9, 18, 27, 36, 45, 54, 63, 72, 81, 90],
[10, 20, 30, 40, 50, 60, 70, 80, 90, 100]]
Krotki¶
Krotki (tuple) to takie listy, których nie możemy modyfikować. Tworzymy je
za pomocą nawiasów okrągłych ().
K_trzyelementowa = (1, 2, 3)
K_jednoelementowa = ('Mielonka',)
K_pusta = ()
W powyższym przykładzie K_trzyelementowa to krotka 3 elementowa
(len(K1) zwróci liczbę 3), K_jednoelementowa to krotka jednoelementowa
a K_pusta to krotka pusta. Proszę zwrócić uwagę na obowiązkowy przecinek
podczas tworzenia jednoelementowych krotek. Krotki możemy też łączyć za pomocą
operatora +
Krotki jako obiekty niemodyfikowalne mają bardzo ograniczone metody. Do
dyspozycji mamy tylko metody count oraz index.
Elementu krotki nie można też usunąć poleceniem del. Na razie tyle
informacji nam wystarczy. Przejdziemy do omówienia trzeciego elementu
sterującego, pętli for.
Pętla for¶
Jak wspomniano wyżej, instrukcja ta służy do iterowania (przechodzenia) po elementach sekwencji. Składnia tej pętli jest następująca:
for element in sekwencja:
BLOK_FOR
Taka pętla będzie miała dokładnie len(sekwencja) obrotów, zatem blok
instrukcji pętli wywoła się dokładnie tyle razy, ile mamy elementów sekwencji.
Spójrzmy na przykład.
Możemy też najpierw zadeklarować zmienną, a później po niej iterować:
Oczywiście, w miejsce zmiennej seq możemy wstawić dowolną zmienną o typie
sekwencyjnym, w tym taką, na której przeprowadziliśmy wycinanie:
Funkcje range, xrange¶
Istnieją dwie niezwykle przydatne funkcje tworzące obiekty iterowalne.
Pierwszą z nich jest funkcja range, tworząca listę liczb całkowitych
(formalnie - listę literałów liczbowych o typie int). Wywołanie tej
funkcję ma następującą składnię:
range(start, stop, krok)
przypomina więc składnię wycinania sekwencji. Funkcja ta zwróci nam listę
liczb, poczynając od wartości start, a kończąc na stop - 1 dokładnie
co krok. Np.
wydrukuje liczby 1, 3, 5, 7, 9. Wielkości start oraz krok są
opcjonalne. Jeżeli podamy tylko jedną liczbę A do funkcji range(A)
dostaniemy wszystkie liczby całkowite od 0 do liczby A. Jeżeli podamy
2 liczby, to pierwsza z nich będzie interpretowana jak start, a druga jak
stop. Krok możemy określić tylko podając komplet. Możliwe są oczywiście
wielkości ujemne, w tym ujemny krok. Dzięki temu stworzymy listę liczb
malejących. Musimy tylko pamiętać o tym, żeby wartość początkowa była większa
od końcowej. Po raz stworzonej liście możemy iterować:
Zadanie
Za pomocą funkcji range oraz pętli for znajdź sumę wszystkich liczb podzielnych przez
5 i 7 w zakresie od 2998 do 4444 (powinieneś dostać liczbę 152110).
Druga funkcja xrange, tworzy szczególny typ sekwencji,, zwany
iteratorem. Nie będziemy wchodzić w szczegóły. Wystarczy zapamiętać, że
jeżeli ów iterator jest sekwencją, którą wykorzystujemy w pętli to wynik
działania range czy też xrange będzie taki sam. Używając xrange,
oszczędzamy pamięć, bowiem range tworzy pełną listę w pamięci komputera, a
xrange w każdym kroku iteracji oblicza kolejną wartość, pamiętając jedynie
wartość obecną, krok oraz wartość końcową. Składnia jest identyczna jak
range:
xrange(start, stop, krok)
oraz wykorzystanie argumentów funkcji również jest takie samo.
Wyrażenia break oraz continue¶
Jeżeli oczekujemy przerwania wykonywania pętli w danej chwili, na podstawie
np. spełnienia jakiegoś warunku możemy użyć słowa kluczowego break.
Przerwane zostaje w tym momencie wykonywanie najbardziej zagnieżdżonej pętli.
Dokładnie odwrotne zachowanie ma instrukcja continue. W momencie
napotkania takowej przestaną wykonywać się instrukcje w bloku pętli i nastąpi
kolejny obrót pętli, niezależnie od stanu programu.
Słowniki¶
Sekwencje indeksowane są liczbami. Słowniki indeksowane są kluczami. W innych językach programowania możecie spotkać się z tablicami asocjacyjnymi lub tablicami z haszowaniem. Słowniki tworzymy za pomocą nawiasów klamrowych oraz pary obiektów (klucz, wartość).
slownik_pusty = {}
slownik = {klucz1: wartosc1, klucz2: wartosc2, ...}
Pierwsza linijka tworzy pusty słownik. Druga linijka definiuje słownik o parach klucz: wartość. O słownikach możemy myśleć jako o nieuporządkowany zbiór właśnie takich par. Kluczami mogą być dowolne zmienne o typach niemodyfikowalnych np: liczby, łańcuchy znaków. Kluczem może być i krotka, pod warunkiem, że jej elementy też są niemodyfikowalne. Słowniki posiadają wiele metod, którymi możemy modyfikować dany obiekt, sprawdzać istnienie klucza czy też pobierać pełną listę kluczy czy też wartości. Do elementów słownika odwołujemy się za pomocą klucza, słownik zwróci wtedy wartość, która powiązana jest z danym kluczem. Jeżeli dany klucz nie występuje w słowniku, dostaniemy komunikat o błędzie.
>>> s = {'Mielonka': 100, 'Jajka': 3.55}
>>> s['Mielonka']
100
>>> s['Jajka']
3.55
>>> s['Pomidor']
KeyErrorTraceback (most recent call last)
KeyError: 'Pomidor'
Wracając na chwilę do problemu piłki wyrzucanej w górę na powierzchni ciała niebieskiego (zadanie 103). Aby rozwiązać to zadanie w nieco bardziej eleganckiej formie, możemy zdefiniować słownik przyspieszeń na powierzchniach takich ciał i wykorzystać go do obliczeni,a na jaką wysokość wzniesie się piłka na danych planetach.
Za pomocą operatora przypisania = możemy zarówno nadpisać istniejącą
wartość dla danego klucza, ale i dodać kolejny element:
s = {'Mielonka': 100, 'Jajka': 3.55}
s['Mielonka'] = 120 # nadpisanie wartosci
s['Pomidor'] = 1.20 # dodanie nowej pary 'Pomidor': 1.20
Typ dict posiada wiele innych metod. Jest metoda``s.keys()``, zwracająca
listę wszystkich kluczy, D.values(), zwracająca listę wszystkich wartości,
czy metoda s.has_key(klucz) sprawdzająca czy dany klucz klucz istnieje
w słowniku s. Jest metoda s.clear() usuwająca wszystkie elementy
słownika czy też s.items(), zwracająca pary (klucz, val) w postaci krotki.
Zadanie
Skonstruuj słownik, w którym kluczami będa liczby od 1 do 10, a wartościami kwadraty
odpowiednich liczb
a) użyj pętli for,
b) użyj pętli while.