Napęd różnicowy i odometria¶

Cel ćwiczenia¶

Zapoznanie się z działaniem optycznego enkodera optycznego. Podstawy odometrii.

Wstęp teoretyczny¶

Większość problemów robotyki sprowadza się do prostego pytania: ,,gdzie jestem?’’. Odometria jest podstawową metodą nawigacji robota i polega na przybliżonym określeniu pozycji i orientacji robota w oparciu o wiedzę o ruchu kół pojazdu (robota mobilnego).

Optyczny enkoder obrotowy¶

Optyczny enkoder obrotowy jest przetwornikiem analogowo-cyfrowym zamieniającym kąt obrotu koła na liczbę impulsów elektrycznych. Enkoder absolutny zlicza impulsy (obroty) od włączenia zasilania. Enkoder przyrostowy (inkrementalny) mierzy przyrost drogi kątowej. Znając liczbę impulsów na obrót \(N\), liczbę impulsów w bieżącym kroku \(n'\), liczbę impulsów z poprzedniego kroku \(n\) oraz promień koła \(R\) możemy obliczyć przyrost drogi \(\Delta D\) w bieżącym kroku:

\[\begin{split}\Delta n = n' - n\\ D = 2\pi R \frac{\Delta n}{N}\end{split}\]

Ruch robota w krótkim okresie czasu (pojedynczym kroku czasowym) możemy przybliżyć ruchem po łuku koła. Wtedy droga przebyta przez środek robota jest średnią arytmetyczną dróg prawego i lewego koła (orientacja robota i obu kół jest identyczna – koła nie są skrętne):

\[D_c = \frac{D_r + D_l}{2}\]

Pełen model robota unicycle w czasie dyskretnym wygląda następująco:

\[\begin{split}\left\{ \begin{array}{l} x' = x + D_c \cos{\phi}\\ y' = y + D_c \sin{\phi}\\ \phi ' = \phi + \frac{D_r - D_l}{L} \end{array} \right.\end{split}\]

Model hybrydowy: unicycle+różnicowy¶

Z połączenia modelu różnicowego i modelu unicycle można obliczyć prędkości kół (sygnał sterujący):

\[\begin{split}\begin{array}{l} v_r = \frac{2v+\omega L}{2R}\\ v_l = \frac{2v-\omega L}{2R}\\ \end{array}\end{split}\]

Zachowanie go-to-goal¶

Zachowanie jedź-do-celu składa się z zachowania jedź-w-kierunku wykonywanym tak długo, jak odległość od celu jest większa od zera (z zadaną tolerancją). Sygnałem wymuszającym jest kąt do celu \(r = \psi\) . Problem sprowadza się do robota unicycle jadącego ze stałą szybkością w stanie \((x, y, \phi)\) oraz celu o współrzędnych \((x_g, y_g)\). Wtedy:

\[\begin{split}\begin{array}{l} \psi = atan2(y_g - y, x_g - x)\\ \varepsilon = \psi - \phi\\ \omega = PID(\varepsilon) \end{array}\end{split}\]

Wykonanie ćwiczenia¶

W ćwiczeniu wykorzystany jest robot educator bez zewnętrznych czujników.

Zapoznaj się z symulatorem pysimiam (pythonowym portem matlabowego symulatora Sim.I.Am) oraz symulatorem sobot-rimulator.

Zaprogramuj robota. Staraj się programować obiektowo z rozbiciem poszczególnych funkcjonalności na oddzielnne moduły. Pamiętaj, że program będzie rozbudowywany na kolejnych ćwiczeniach o nowe funkcjonalności. Robot inicjalizuje się na pozycji o współrzędnych \((0,0)\) o orientacji \(\phi=0\). Ruch robota zadajemy metodą \(run(v, \omega)\), gdzie \(v\in [-100,100]\) jest szybkością robota (nie można jej zadać dowolnie, zależy od parametrów kół, maksymalnej prędkości silników oraz \(\omega\)) a \(\omega\in [-100,100]\) jest szybkością kątową. Robot na bieżąco oblicza swoją pozycję i orientację (odczytując wartości encoderów). Używając wersji systemu jesse Można wykorzystać (lub zmodyfikować) metodę steering:

def steering(direction, power=500):
    """
    Computes how fast each motor in a pair should turn to achieve the
    specified steering.
    Input:
        direction [-100, 100]:
            * -100 means turn left as fast as possible,
            *  0   means drive in a straight line, and
            *  100 means turn right as fast as possible.
        power: the power that should be applied to the outmost motor (the one
            rotating faster). The power of the other motor will be computed
            automatically.
    Output:
        a tuple of power values for a pair of motors.
    Example::
        for (motor, power) in zip((left_motor, right_motor), steering(50, 100)):
            motor.run_forever(speed_sp=power)
    """

    pl = power
    pr = power
    s = (50 - abs(float(direction))) / 50

    if direction >= 0:
        pr *= s
    else:
        pl *= s

    return (int(pl), int(pr))

Oprogramowanie w wersji stretch ma już zaimplementowane klasy MoveTank i MoveSteering. Dokładny opis znajduje się w dokumentacji.

Zachowanie go_to_goal \((x_g, y_g)\) do sterowania wykorzystuje regulator PID, jednak początkowo parametry \(k_I\) i \(k_d\) ustawiamy na zero, czyli wykorzystujemy jedynie regulator proprocjonalny. Dopiero po przetestowaniu, że robot działa prawidłowo dostrajamy pozostałe parametry.

Wywołanie głównej części programu powinno mieć postać zbliżoną do:

waypoints = [[x_1, y_1], [x_2, y_2], ..., [x_n, y_n]]
for goal in waypoints:
    robot.go_to_goal(goal)
robot.stop()

Przetestuj robota na torze, schemat którego znajduje się na rysunku. Robot ma ruszać z boksa startowego o współrzędnych \((0,0)\) i orientacji \(\phi=0\), przejechać przez pierwszy punkt kontrolny o współrzędnych \((200,0)\) (marker powinien przejść między kołami robota), przejechać przez drugi punkt kontrolny \((125, 100)\) a następnie zatrzymać się w boksie docelowym o współrzędnych \((125, 200)\). Jeśli wszystko zadziała, to orientacja robota będzie wynosiła \(\phi = \pi/2\). Współrzędne są podane w centymetrach.
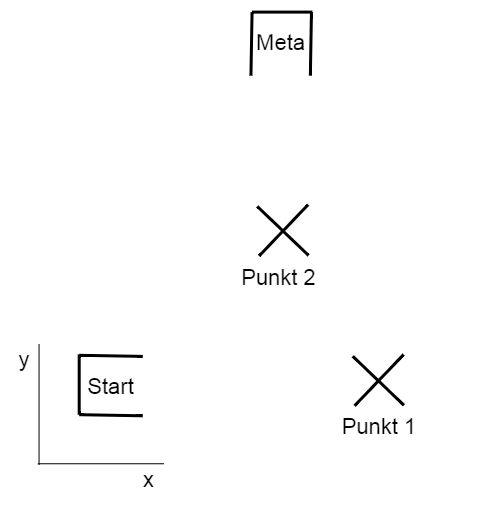
Czas przejazdu robota zapisz w tabeli.

Opis sprawozdania¶

Sprawozdanie z ćwiczenia powinno zawierać:

Opis implementacji algorytmu.
Listingi programów (pliki .py i/lub .ev3) z optymalnymi wartościami parametrów.
Tabelka z wynikami (czas przejazdu oraz odległość robota od celu po zatrzymaniu (odległość mierzymy od dalszego koła do najbliższej krawędzi kratki). Jeśli robot obydwoma kołami zatrzyma się wewnątrz kratki, wpisujemy \(0\)).
Wnioski – dyskusja wyników.

Next Section - Robot omijający przeszkody