Lekcja 9. Kilka ciekawych problemów¶
Zbliżamy się już do końca. Przed nami lekcja w zasadzie podsumowująca zajęcia w projekcie od Algorytmu do Zawodowca. Poznacie tutaj kilka ciekawych algorytmów. Postarajcie się samodzielnie zaprojektować programy je realizujące. Jeżeli odpowiada wam język Python to świetnie, ale nic się nie stanie jeżeli zdecydujecie się na jakikolwiek inny.
Mnożenie¶
Na początek w miarę proste zagadnienie - mnożenie dwóch liczb. W dodatku
będziemy zakładali, że jedna z nich jest liczbą naturalną c. Druga jest w
zasadzie dowolna, może być całkowita, może rzeczywista. Nazwiemy ją x.
Zadanie polega na wymnożeniu ich przez siebie. Oczywiście - nic prostszego.
Piszemy szybko
>>> c * x
i uzyskujemy odpowiedź. No dobra, ale co w przypadku, gdy nie wiemy co to
znaczy *? Powstaje pytanie: jak wymnożyć przez siebie takie liczby bez
używania mnożenia? Jeżeli c jest liczbą całkowitą to oczywiście możemy
liczbę x dodać do siebie c razy. To jest wasze pierwsze zadanie
Zadanie 9.1
Napisz algorytm mnożący ze sobą liczbę całkowitą c oraz liczbę x
bez używania mnożenia. Użyj do tego dowolnej techniki - może być diagram,
pseudokod - jak tylko chcesz.
Zadanie 9.2
Zaimplementuj właśnie stworzony przez siebie algorytm.
Istnieje też inna metoda wykonania takiego mnożenia. Metoda znana jest jako metoda mnożenia rosyjskich chłopów. Algorytm ten również będzie bazował na dodawaniu do siebie liczb, z tym, że zmniejszymy wyraźnie liczbę tych sumowań. Algorytm podamy w postaci zwykłego przepisu.
Mnożenie rosyjskich chłopów
- Stwórz dwie listy
L1orazL2. Do jednej na pierwszym miejscu wpiszcdo drugiejx.- Jeżeli ostatnia wartość listy
L1wynosi1to przejdź do punktu 5. Jeżeli jest większa to przejdź do kroku 3.- Weź ostatnią wartość z listy
L1.- Jeżeli jest parzysta to weź jej połowę i wpisz jako kolejną wartość
L1. Jeżeli nieparzysta to najpierw odejmij liczbę1, dopiero potem wpisz połowę zredukowanej wartości doL1. W drugiej liścieL2wpisz podwojoną wartość ostatniego jej elementu.- Dodaj do siebie wszystkie liczby z listy
L2którym w liścieL1odpowiadają liczby nieparzyste.- Zwróć wynik sumowania z punktu 5. Jest to wynik iloczynu \(c\cdot x\).
Podamy teraz przykład, tak, żeby łatwiej było zrozumieć algorytm. Powiedzmy, że chcemy wykonać mnożenie \(67 \cdot 412\). Tak więc po kolei:
| L1 | L2 |
|---|---|
| 67 | 412 |
| 33 | 824 |
| 16 | 1648 |
| 8 | 3296 |
| 4 | 6592 |
| 2 | 13184 |
| 1 | 26368 |
I na końcu sumowanie \(412 + 824 + 26363 = 27604 = 67 \cdot 412\). Łatwe prawda? Dodatkowo wykonujemy 7 przepołowień i 7 dodawań by zbudować listy, potem wykonujemy 7 decyzji czy zostawić liczbę z listy 2 czy nie a na końcu zostają nam raptem 2 dodawania by uzyskać wynik. To zdecydowanie mniej niż 66 dodawań z pierwszego algorytmu mnożenia bez mnożenia.
Zadanie 9.3
Stwórz schemat blokowy na bazie powyższego algorytmu.
Zadanie 9.4
Zaimplementuj algorytm mnożenia rosyjskich chłopów.
- w wersji podstawowej możesz korzystać z mnożenia i dzielnia z użyciem
liczby
2. - w wersji finalnej powinieneś unikać operatorów
*oraz/.
Zadanie 9.5
Zmień program tak, aby móc mnożyć również liczby całkowite i rzeczywiste. Jak poradzisz sobie ze znakiem?
Szyfrowanie¶
Z szyfrowaniem wiadomości mamy do czynienia na codzień, czy to wysyłając
emaila, czy używając bezpiecznych stron internetowych dzięki protokołowi
https. Na przykład serwer Jupyter dedykowany zajęciom w ramach projektu Od
algorytmu do zawodowca wykorzystuje właśnie taką zabezpieczoną wersję
protokołu http. Problem ukrywania rzeczywistych wiadomości za pomocą szyfru
jest znany od wieków. Istnieje wiele rodzajów szyfrowania. Tutaj omówimy
prosty, naiwny wręcz szyfr Cezara. Pomimo prostoty daje on jednak łatwość
zrozumienia idei jakie stoją za pewną ogólną techniką szyfrowania
podstawieniowego.
W metodzie podstawieniowej dany znak wiadomości zastępuje się innym, ale zawsze
takim samym znakiem. Przykładowo ciąg znaków szyfr możemy zastąpić poprzez
ciąg liczb 18 25 24 5 17. Jak łatwo się domyślić ciąg ten odpowiada
miejscom liter w alfabecie. Klucz do rozszyfrowania powyższego ciągu to po
prostu ciąg znaków zawierający alfabet. Wystarczy odwołać się do odpowiednich
indeksów
Szyfr Cezara¶
W przypadku szyfru Cezara, zwanego też szyfrem przesuwającym, w miejsce danego znaku wiadomości podstawiamy inną literę alfabetu oddaloną od oryginalnej litery o stałą liczbę pozycji w alfabecie. Biorąc litery do podstawienia przesuwamy się zawsze w tym samym kierunku. Jeżeli dojdziemy do końca alfabetu, to wracamy na początek. Poniżej znajdziecie ilustrację szyfru Cezara o przesunięciu 3:
Alfabet: a|b|c|d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z
Szyfr: d|e|f|g|h|i|j|k|l|m|n|o|p|q|r|s|t|u|v|w|x|y|z|a|b|c
Sam algorytm szyfrowania jest bardzo prosty (jest to tylko jedna z możliwości)
- Wybierz przesunięcie P,
- Stwórz szyfr zastępując każdą literę alfabetu inną literą, przesuniętą względem oryginalnej o stałą liczbę pozycji w alfabecie,
- Zastosuj podstawienie.
Co daje nam dość prosty kod w języku Python. Szyfruje on jednak tylko litery z alfabetu łacińskiego.
Zadanie 9.6
Przepisz powyższą funkcję szyfruj tak, aby zamiast słownika
wykorzystywała bezpośrednio łańcuch znaków AL. Może przydać się funkcja
zwracająca resztę z dzielenia.
Problem odwrotny, czyli łamanie szyfru Cezara też nie stanowi jakiegoś większego wysiłku
algorytmicznego. Jest to po prostu siłowa metoda sprawdzania kolejnych możliwych przesunięć
i odczytywanie tak wygenerowanej wiadomości. Co ciekawe, można do tego użyć dokładnie tej samej
funkcji szyfr, którą już napisaliśmy. Potrzeba tylko cierpliwości, bo ktoś musi na owe
wygenerowane ciągi znaków patrzeć i w pewnym momencie powiedzieć eureka!.
Zadanie 9.7
Napisz algorytm łamania szyfru Cezara.
Zadanie 9.8
Napisz program realizujący właśnie napisany algorytm.
W rzeczywistości oczywiście nikt nie siedzi przy tekście i nie patrzy czy dany szyfr został już złamany. Od tego również jest komputer, nie trzeba wpatrywać się w odszyfrowany tekst. Wystarczy napisać program by to robił za nas. Oczywiście Python będzie “wpatrywał się” poprzez porównywanie podciągów pomiędzy spacjami, czyli poprzez porównywanie słów z jakimś zbiorem słów (słownikiem). Jeżeli jeszcze jesteś zainteresowany deszyfrowaniem, to będzie to twoje kolejne zadanie.
Zadanie 9.9
Ze strony http://sjp.pl/slownik/odmiany/ możecie pobrać archiwum zip polskich słów. Plik ten może służyć do porównywania, czy odkodowane słowo jest poprawnym słowem w języku polskim. Użyj tego pliku do napisania programu automatycznie sprawdzajacego, czy odszyfrowane słowa są poprawnymi słowami polskimi. Zaprojektuj ten program. Naszkicuj algorytm - narysuj schemat blokowy albo użyj pseudokodu, potem postaraj się napisać prostą, zrozumiałą wersję programu. W końcowej fazie możesz poprawiać kod. To zadanie może zająć chwilę...
Na koniec ciekawostka - szyf Cezara jest współcześnie używany w internecie! Jest to tzw. ROT13. Alfabet łaciński składa się z 26 liter, czyli szyfr Cezara z przesunięciem o \(26/2=13\) będzie szyfrem symetrycznym (to znaczy przesunięcie o \(13\) znaków w prawo albo w lewo da nam ten sam wynik. A dwukrotne szyfrowanie (czyli zaszyfrowanie zaszyfrowanego tekstu) da nam początkowy, odszyfrowany, tekst.
Szyfru ROT13 używa się wtedy, gdy chcemy nieświadomego czytelnika uchronić przed przypadkowym przeczytaniem tekstu. Wyobraźmy sobie, że czytamy forum miłośników filmu, gdzie trwa dyskusja o nowym odcinku ulubionego serialu. Część użytkowników forum już go widziała, pozostali jeszcze nie. Wszystkie informacje mogące “zaspojlerować” przyjemność oglądania możemy zaszyfrować ROT13. Chętni sobie odszyfrują, pozostali mogą ten fragment ominąć. Metoda ta jest na tyle popularna, że istnieją wtyczki do przeglądarek, automatycznie “rotujące” tekst.
Problem komiwojażera - studium przypadku¶
Jednym z ważnych obszarów wiedzy powiązanych z algorytmiką jest dział matematyki (i jednocześnie informatyki) zwany teorią grafów.
Czym są grafy? W definicji matematycznej natrafimy na informację, że przez graf rozumiemy zbiór wierzchołków połączonych krawędziami. Wierzchołki reprezentują jakieś obiekty, a krawędziom możemy przypisać relacje pomiędzy tymi obiektami. Czym są takie grafy w praktyce? Za pomocą grafów możemy reprezentować na przykład: schematy połączeń drogowych i kolejowych, topologie sieci komputerowych, schematy obwodów elektrycznych, itp. Innymi słowy, grafy służą do ilustrowania relacji między obiektami.
Początki teorii grafów sięgają 1736 roku, w którym to bardzo znany matematyk – Euler zajmował się rozwiązaniem ciekawego, realnego problemu. Mieszkańcy Królewca głowili się nad tym, jak pokonać wszystkie siedem znajdujących się w mieście mostów, tak by przez żaden z nich nie przechodzić dwa razy. Za pomocą wierzchołków można zaprezentować wszystkie cztery fragmenty Królewca porozdzielane rzekami, a za pomocą krawędzi - mosty je łączące.
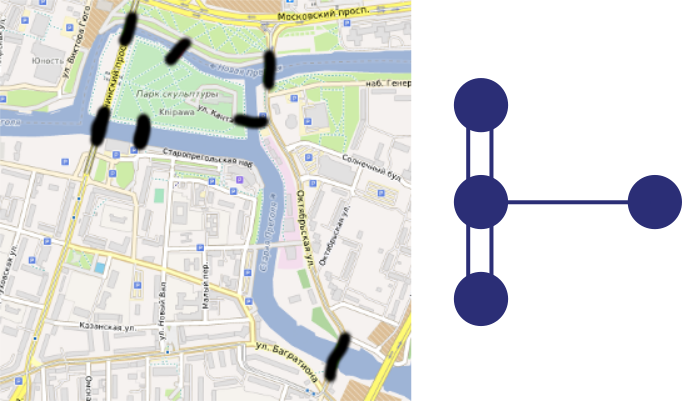
Rozmieszczenie mostów w Królewcu. Graf opisujący zagadnienie.
Teoria grafów jest bardzo obszerną dziedziną. Z punktu widzenia informatyki, a w szczególności algorytmiki, grafy to nic innego jak pewna struktura danych.
Niniejszy akapit ma na celu zaprezentowanie i krótkie omówienie jednego ze słynniejszych problemów teorii grafów/algorytmiki - tak zwanego problemu komiwojażera (ang. traveling salesman problem). Jest to tak zwany problem NP-zupełny. Co to jest problem NP-zupełny? W bardzo dużym uproszczeniu to takie zagadnienie, dla którego nie można znaleźć algorytmów dających dokładne rozwiązanie w czasie (wielomianowym) zależnym od wielkości danych.
Sformułowanie problemu komiwojażera brzmi następująco:
Załóżmy, że jesteśmy przedstawicielem handlowym (komiwojażerem). Dysponujemy listą miast, z których każde musimy odwiedzić, ale każde tylko i wyłącznie raz. Jednocześnie chcemy pokonać jak najkrótszą drogę. Chcemy również na końcu wrócić do miejsca startu.
Spróbujmy przyjrzeć się jak ten problem będzie wyglądał dla czterech miast:
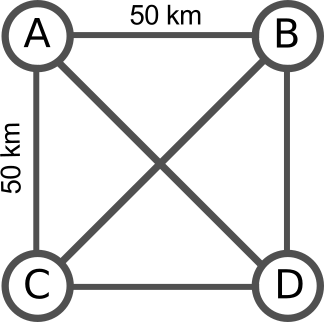
Graf dla czterech miast w topologii kwadratu.
Wierzchołki reprezentują cztery miasta, oznaczane odpowiednio A, B,
C oraz D. Miasta te rozmieszcozne są w wierzchołkach kwadratu o boku 50
km (dla uproszczenia przyjmijmy, że długość przekątnej tego kwadratu wynosi 70
km). Odległość od miasta A do miasta B jest taka sama jak odległość od
miasta B do miasta A. Nie, nie ma poprzednim zdaniu błędu. Odpowiada
to sytuacji, w której problem komiwojażera nazywac będziemy symetrycznym. Można
sformuować problemy asymetryczne. Zazwyczaj zgodne z intuicją jest myślenie, że
odległość z Katowic do Krakowa jest taka sama w obie strony. Gdybyśmy
chcieli jednak optymalizować nie drogę, a na przykład zużycie paliwa, to możemy
dojść do asymetrycznego problemu komiwojażera. Do Katowic z Krakowa
może być z górki, a co za tym idzie w odwrotną stronę pod górkę. A to ma wpływ
na spalanie, koszta, etc.
W grafach ciąg wierzchołków, w których każde dwa kolejne są połączone krawędzią nazywamy drogą/ścieżką. Z kolei cyklem nazywamy taką drogę, która kończy się w tym samym wierzchołku, w którym się zaczęła.
Przyjmijmy, że startujemy w mieście A. Dla powyższej topologii istnieje 6
niezależnych cykli:
- A->B->C->D->A
całkowita długość przebytej drogi:
\[50+70+50+70=240 \textrm{ [km]}\]
- A->B->D->C->A
całkowita długość przebytej drogi:
\[50+50+50+50=200 \textrm{ [km]}\]
- A->C->B->D->A
całkowita długość przebytej drogi:
\[50+70+50+70=240 \textrm{ [km]}\]
- A->C->D->B->A
całkowita długość przebytej drogi:
\[50+50+50+50=200 \textrm{ [km]}\]
- A->D->B->C->A
całkowita długość przebytej drogi:
\[50+70+50+70=240 \textrm{ [km]}\]
- A->D->C->B->A
całkowita długość przebytej drogi:
\[50+70+50+70=240 \textrm{ [km]}\]
Nie jest trudno zauważyć, że przy takim ułożeniu miast wystarczy unikać przekątnych (po prostu poruszać się po obwodzie kwadratu) by droga była najkrótsza. Możemy rozważać inne wzajemne ułożenie miast. Z innymi odległościami między nimi.
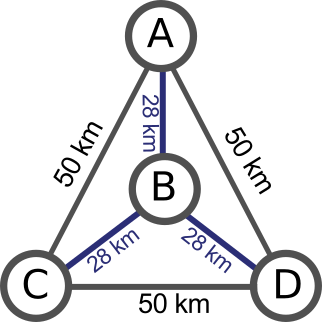
Graf z inną topologią ułożenia miast.
Dla drugiego grafu, również będzie istniało 6 cykli. Naturalnie, inne jednak będą długości uzyskanych dróg.
Ponieważ mamy ustalony węzeł początkowy, to pozostałe trzy miasta możemy ustawić w permutacje na \(3!\) sposobów. W ogólności dla problemu z \(n\) miastami ilość cykli wynosi \((n-1)!\). Z tej liczby bierze się poziom komplikacji całego problemu! Nie jest trudno wyobrazić sobie kuriera, który ma w ciągu dnia rozwieźć jedynie 15 paczek. Może to zrobić, na ... jedyne 87178291200 sposobów, bo tyle wynosi \(14!\).
Zagadka komiwojażera jest rozwiązywalna znaną już z tego kursu metodą siłową. Polega ona na sprawdzeniu wszystkich możliwych cykli i wyszukaniu dla którego/których z nich droga jest najmniejsza. Jeszcze jedna z uwag: cykl w którym dany wierzchołek odwiedzamy tylko raz, nazywany jest w teorii grafów cyklem Hamiltona. Zatem można powiedzieć, że rozwiązanie tego problemu metodą brute force polega na sprawdzeniu wszystkich jego ścieżek Hamiltona.
Zdanie 9.10
Biorąc pod uwagę cztery miasta zaproponuj algorytm rozwiązania siłowego problemu komiwojażera w postaci pseudokodu.