Lekcja 5. Podejście algorytmiczne¶

Programy i ich opis¶

Niezależnie od tego jak technicznie podejdziecie do problemu, jego rozwiązanie zawsze będzie pewną sekwencją instrukcji czy operacji prostych. Tu i ówdzie wykorzystacie pętlę, gdzie indziej funkcję. Taki ciąg jasno określonych czynności, prowadzących do wykonania zadania nazywamy właśnie algorytmem. Klasyczną definicję algorytmu można znaleźć w Wikipedii

Algorytm

to jednoznaczny przepis przekształcenia w skończonym czasie danych wejściowych do danych wynikowych

Aby podać dany algorytm możemy posłużyć się jednym z wielu zapisów. Załóżmy, że chcemy napisać program obliczający wartość bezwzględną liczby a. Nie jest to specjalnie trudne. W Pythonie będzie to wyglądać tak

Aby podać algorytm obliczania takiej funkcji (nazywamy ją tradycyjnie modułem |a| liczby) możemy posłużyć się opisem słownym algorytmu

1. mamy liczbę \(a\),
2. dla liczb dodatnich \(a \ge 0\) zwróć \(a\),
3. dla liczb ujemnych \(a < 0\) zwróć \(-a\).

Czasami można po prostu podać wzór matematyczny. Dla naszej funkcji będzie on wyglądał tak

Możemy też podać listę niezbędnych kroków do uzyskania prawidłowego wyniku.

1. pobierz literał liczbowy a,
2. jeżeli a >= 0 zwróć a; zakończ program,
3. w innym przypadku zwróć -a; zakończ program.

Kolejną możliwością jest podanie przepisu w postaci schematu blokowego. Dla naszej funkcji będzie on wyglądał tak

Funkcja modulo - schemat blokowy.

Niezależnie od tego, w jakim języku programujemy powyższy schemat będzie nam mówił, jaką strukturę powinien mieć program, aby obliczał liczbę bezwzględną. To właśnie cechuje dobry algorytm - powinien on określać przepis niezależnie od preferowanego języka programowania. Przypatrzmy się jak jest on zbudowany. Strzałki określają kolejność operacji: zaczynamy tam gdzie start, nastepnie pobieramy liczbę do zmiennej a i przechodzimy do rozgałęzienia. Tam decydujemy czy \(a \ge 0\) po czym następuje zwrot liczby a, czy też warunek nie jest spełniony i zwracamy odwrotność liczby -a. Po zwrocie następuje zakończenie programu.

W takim schemacie możemy znaleźć

• strzałka – wskazuje jednoznacznie powiązania i ich kierunek,
• operand – prostokąt, do którego wpisywane są wszystkie operacje z wyjątkiem instrukcji wyboru,
• predykat – romb, do którego wpisywane są wyłącznie instrukcje wyboru,
• etykieta – owal służący do oznaczania początku bądź końca sekwencji schematu (kończy, zaczyna lub przerywa/przenosi schemat).

Jeżeli chcesz dowiedzieć się więcej, to odsyłamy do artykułu na wikipedii.

Ostatnią możliwością o której wspomnimy (choć nie wyczerpujemy zagadnienia) to możliwość prezentacji algorytmu za pomocą pseudokodu. Najpierw przykład:

ABSOLUTE_VALUE(a)
  if a >= 0
      return a
  else
      return -a

Pseudokod jest (i powinien być) bardzo podobny do programu komputerowego - porównaj ActiveCode 1 na początku lekcji. Nie ma jakiś szczególnych zaleceń co do składni takiego pseudo-kodu. Równie dobrze moglibyśmy użyć języka polskiego:

WARTOSC_BEZWZGLEDNA(a)
  jeżeli a >= 0
      zwróć a
  w innym przypadku
      zwróć -a

Pierwszy pseudokod jest zgodny z tym prezentowanym we Wstępie do algorytmów Thomasa Cormena [TC] (swoistej biblii programistów). Drugi to wolne tłumaczenie tego pierwszego. Oba są zrozumiałe, oba pozwolą wam napisać program realizujący funkcję zwracającą moduł liczby a. Zachęcamy właśnie do tej ostatniej postaci prezentacji własnych algorytmów. Często spisanie czegoś na kartce papieru znacznie ułatwia rozwiązanie. Późniejsza implementacja jest z reguły łatwa.

Analiza programów¶

Każdy problem jaki stanie przed programistą może być zazwyczaj rozwiązany na kilka sposobów. Zobaczmy na przykład. Załóżmy, że chcemy policzyć silnię liczby naturalnej n. Wiemy, że

Możemy zatem napisać program bazując na algorytmie iteracyjnym:

SILNIA(n)
    i = 1
    sil = 1
    dopóki i <= n
        pomnóż sil przez i
        podnieś i o 1
    zwróć sil

co po przetłumaczeniu tego algorytmu na język Python da nam następujący program

Możemy też spojrzeć na problem nieco inaczej i przedstawić silnię jako

i zapisać to jako program rekurencyjnie:

RSILNIA(n)
    jeżeli n < 1
        wynik = 1
    w innym przypadku
        wynik = n * RSILNIA(n - 1)
    zwróć wynik

Da to znane już z lekcji o funkcjach rekurencyjne rozwiązanie

Oba wyniki są identyczne, bo w obu przypadkach 5!=120. Z punktu widzenia programisty są to zupełnie inne programy, wykorzystujące inną technikę programowania. Można sobie zadać pytanie? Który z nich jest lepszy? Może pierwszy, może drugi, a może żaden? Najpierw trzeba by określić kryteria na których podstawie powinniśmy oceniać programy. Mogą to być

• liczba operacji prostych niezbędnych do wykonania programu
• czas działania programu
• zapotrzebowanie na pamięć
• czas potrzebny do napisania kodu
• wygląd samego kodu

Trzy pierwsze kryteria są raczej oczywiste. Każdy chce napisać program, który przy wykorzystaniu minimalnych zasobów maszyny zwróci wynik w naj najszybszym czasie. Można to osiągnąć stosując np. triki czy zaawansowane techniki programistyczne. Prawda jest jednak taka, że szybkość działania programów zależy przede wszystkim od algorytmu użytego do rozwiązania problemu. Technika programistyczna jest drugorzędna, choć na pewno ma też wpływ na sam program.

Kryterium czwarte, to mówiące o czasie jaki spędzimy nad projektowaniem i tworzeniem samego programu nie jest takie oczywiste. Czasami musimy rozwiązać jakiś problem szybko, na wczoraj. Wyobraźmy sobie 2 scenariusze

1. używamy siłowych technik i poświęcamy 3 godziny na napisanie programu, który później w 1 dzień pracy zwróci nam (prawidłową) odpowiedź
2. projektujemy skomplikowany algorytm w 1 dzień, kolejny dzień poświęcamy na programowanie i testy, i znajdujemy odpowiedź w 10 minut pracy maszyny

Którą metodę wybrać? To już zależy od was, a może przede wszystkim od celu jaki sobie postawicie. Jeżeli problem jest jednorazowy to lepiej nie tracić na niego czasu - niech się męczy komputer - wybieramy opcję (a). Jeżeli wiecie, że zagadnienie będzie powracać co jakiś czas, to może warto poświęcić mu 2 dni pracy, by później mieć efekty w 10 minut...

I w końcu ostatni punkt. Z pozoru najmniej istotny. Jakie bowiem ma znaczenie, czy program realizujący silnię napiszę tak jak wyżej w ActiveCode 2 czy może tak

Widzicie różnicę? Oba programy działają identycznie, czyli poprawnie obliczają silnię z podanej jako argument liczby. Pierwszy ten z początku lekcji jest jednak czytelny, ten powyżej trochę mniej... Starajcie się raczej programować czytelnie. Pomagają w tym zarówno komentarze, jak i wcięcia (obowiązkowe w Pythonie) czy nazwy obiektów - zmiennych, funkcji i klas.

Aby formalnie stwierdzić który z algorytmów przez nas zaprojektowanych będzie wymagał większej ilości instrukcji, a co za tym idzie pochłonie więcej zasobów CPU, musimy poznać metodę opisu algorytmów charakteryzującą ich złożoność obliczeniową.

Złożoność obliczeniowa¶

Tak naprawdę każdego z nas najbardziej interesuje jak szybko pracuje dany program komputerowy oraz jakie zasoby sprzętowe będę potrzebne do jego stabilnej pracy. Aby określić czas pracy danego programu można sprawdzić czas jego działania za pomocą stopera. Nie jest to jednak najlepsza metoda. W zależności od komputera stoper może pokazać 2 godziny albo 2 minuty, a przecież uruchamiamy ten sam program! Zerknijmy na program obliczający sumę elementów prostego szeregu arytmetycznego

Poniższy kod oblicza sumę częściową ciągu, czyli sumę N elementów. Aby sprawdzić czas wykonania za pomocą stopera użyjemy modułu time.

Teraz proste wywołanie funkcji prosty_ciag(1000) zwróci nam milion, oraz czas wykonania programu (czas może się różnić w zależności od maszyny).

print prosty_ciag(1000)
1000000, 0.006495

Na początku uruchomimy ten program kilka razy dla N = 1000000.

Jak widać za każdym razem czas uruchomienia programu jest inny, ale bardzo do siebie zbliżony. Mówimy, że rząd wielkości jest taki sam. Teraz uruchomimy ten program dla kilku różnych wartości N.

Jak widać, teraz czas wydłuża się dziesięciokrotnie (no, prawie...) jeżeli dziesięciokrotnie zwiększymy N. Im większe N tym dłużej maszyna musi obliczać sumę ciągu. Jest to ogólna charakterystyka programów - zależą one w dużej mierze od danych wejściowych. Trzeba to zapamiętać.

Czas wykonywania programu (algorytmu) zależy od wielkości danych wejściowych.

Do problemu sumy częściowej możemy też podejść nieco inaczej. Taką sumę częściową można obliczyć. Jeżeli mamy N wyrazów ciągu \(\{a_i\}_{i=1}^N\), o kroku równym r, to

co w naszym przypadku dla r=2 oraz \(a_1 = 1\) da

Napisanie programu obliczającego taką sumę nie będzie bardzo trudne.

Możemy teraz przeprowadzić podobne testy, które wykonaliśmy dla poprzedniej wersji programu, tej liczącej sumę częściową za pomocą pętli. Również i teraz oszacujemy czas potrzebny do obliczenia jej dla kilku różnych wielkości danych wejściowych N (czyli liczby elementów ciągu).

Jak widzimy, wszystkie czasy są zbliżone - są niezależne od podanej wielkości N. Są też bardzo krótkie w porównaniu z tymi dla wersji z pętlą. Jak widać użycie innego (odpowiedniego) algorytmu do rozwiązania jakiegoś problemu jest w stanie zdecydowanie przyspieszyć nasz program. Warto zapamiętać

Czas wykonania programu zależy od wybranego algorytmu.

Czas wykonywania programu można klasyfikować poprzez podanie ilości operacji prostych (takich jak dodawanie, wywołanie funkcji czy odczytanie elementów listy). Przykładowo program jaki widnieje w ActiveCode 9 będzie miał takich instrukcji kilka (zdefiniowanie funkcji, zaimportowanie modułu time, odejmowanie...). Program z ActiveCode 5 nieco więcej. Przede wszystkim ich ilość będzie zależeć od N, ponieważ tyle razy wykona się instrukcja z bloku pętli while - im większe N tym więcej instrukcji prostych (mnożenia, odejmowania, dodawania, przypisania) będzie musiało się wykonać. W przypadku, jeżeli N jest małe (np: 3), to liczba innych instrukcji, tych poza pętlą while będzie miała znaczenie. Jeżeli weźmiemy pod uwagę milion elementów ciągu, to te kilka instrukcji (import, pomiar czasu) nie będzie już miało większego znaczenia - nie będzie bowiem wielkiej różnicy czy wykonamy takich instrukcji 1000000 czy 1000005.

Wskazówka

Notacja “duże O”

Do określenia zachowania się algorytmu właśnie dla dużych danych wejściowych posługujemy się pewną teoretyczną miarą opisującą asymptotyczną złożoność obliczeniową, opisującą jak szybko rośnie czas wykonania programu, jeżeli zwiększać będziemy wielkość danych wejściowych. Do opisu tej zależności stosujemy notację dużego O oraz jej modyfikacje. Mówi ona o tym, że tempo wzrostu \(f\) jest co najwyżej rzędu danego przez funkcję \(g\), jeżeli istnieją dwie stałe \(n_0 > 0\) oraz \(c > 0\), takie, że

\[\begin{split}\forall n > n_0: f(n) \le c g(n)\end{split}\]

i zapisujemy

\[f(n) \in O(g(n))\]

Mówimy wtedy, że tempo wzrostu czasu wykonania programu jest rzędu \(O(f(n))\). Przykładowo złożoność obliczeniowa programu z ActiveCode 5 jest liniowa dla N. Mówimy wtedy, że jest \(O(N)\). W przypadku programu z ActiveCode 9 mamy do czynienia ze stałą złożonością obliczeniową. Wtedy szybkość działania programu jest niezależna od podanego N. Taką sytuację oznaczamy zapisem \(O(1)\). Jak widać nie musimy dokładnie takiego tempa określać, wystarczy, że podamy rząd wielkości (w postaci funkcji). Tutaj znajdziecie najbardziej typowe złożoności

f(n)	złożoność
\(1\)	stała
\(\log n\)	logarytmiczna
\(n\)	liniowa
\(n \log n\)	liniowo - logarytmiczna
\(n^2\)	kwadratowa
\(n^c\)	wielomianowa
\(c^n\)	wykładnicza

Możemy też zerknąć na wykresy tych funkcji, aby uświadomić sobie jaka jest między nimi różnica.

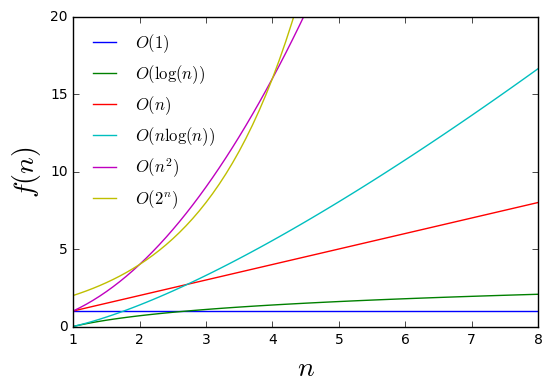
Popularne tempa wzrostu

Nie zaprzątając sobie zbytnio głowy powyższymi definicjami, aby określić jakie tempo wzrostu ma dany program zawsze możemy zmierzyć czas podobnie jak robiliśmy to powyżej, takie czasy wyświetlić tabelarycznie lub zmagazynować je w liście by w końcu wykreślić ich wykres. Może nie od razu wpadniemy na to, jaka jest złożoność obliczeniowa programu, ale na pewno będziemy w stanie określić, w którym przypadku program działa szybciej - im wyrysowana funkcja rośnie szybciej tym wolniej działa program.

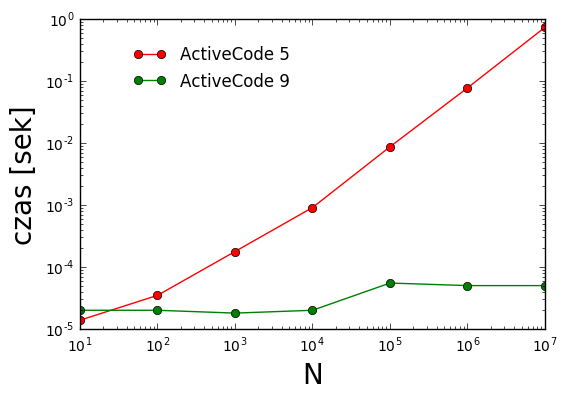
Wykres czasu działania programów omówionych powyżej. Zwróć uwagę na podwójnie logarytmiczny wykres!

O tym jak rysować takie funkcje dowiesz się na lekcji oraz z dodatku 3.