The conic sections¶

Preparing for this tutorial:¶

The LEGO Robot that coincides with this tutorial comes from building specific sections found in the LEGO® MINDSTORMS® Education EV3

Core Set building instructions. You will need to build the main body for the robot, adapted to draw with some pen.

Time constraints:

• starting from 90 min + 90 min

Exercise¶

1. Create a program that will cause the robot to plot an ellipse to be determined by \(\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\).

2. Plot an ellipse: \(\frac{x^{2}}{16} + \frac{y^{2}}{49} = 1\).

3. Plot a circle with a given radius.

4. How large must the radius of the inner circle be to have a right wheel three times the speed of a left wheel?

Theory¶

In mathematics, there are different kinds of functions and we know different equations of functions. One of them is the parametric equation. We will deal primarily with this equation.

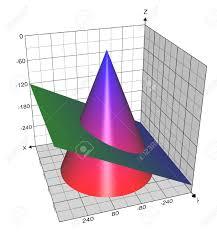
The conic sections a circle, an ellipse, a hyperbola and a parabola are obtained as the intersection of a cone with the plane.

Let’s investigate an ellipse.

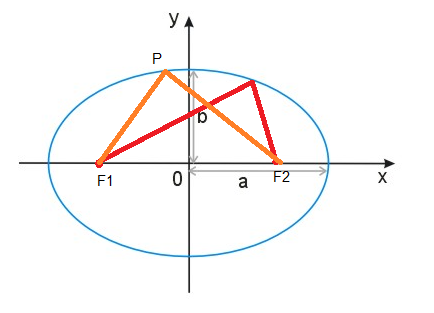
An ellipse is a plane curve surrounding two focal points (denoted by F1, F2), such that for all points on the curve, the sum of the two distances to the focal points is a constant (|F1P|+|F2P|=const). As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same point (F1=F2).

The equation of a standard ellipse centered at the origin with width 2a and height 2b is:

\(\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1\) d(F1,P)+d(F2,P)=2a d-distance

Assuming a ≥ b, the focal points are F(±c, 0) for \(c = \sqrt{a^2-b^2}\).

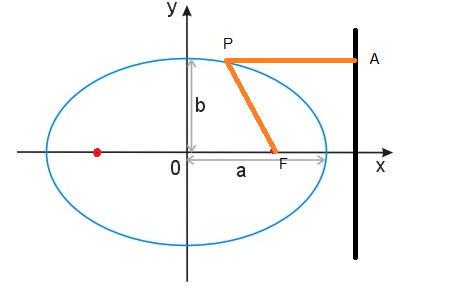
An ellipse may also be defined in terms of one focal point and a line outside the ellipse called the directrix: for all points on the ellipse, the ratio between the distance to the focus and the distance to the directrix is a constant:

• \(e = \frac{c}{a} = (\frac{|PF|}{|PA|})\) numerical eccentricity

  

To plot ellipses we will use polar coordinates.

In polar coordinates, with the origin at one focus, with the angular coordinate measured from the major axis the ellipse’s equation is \(r(\theta) = \frac{a(1 - e^{2})}{1 \pm \text{e cos }\theta}\). It could be also writing as

\(r(\theta) = \frac{p}{1 - \varepsilon \bullet cos\theta}\), where

• p is the ordinate of the point above the focus F(c,p)

• \(\varepsilon = \frac{e}{a}\) numerical eccentricity (for ellipse)

  \(\varepsilon < 1\)- for circle \(\varepsilon = 1\) )

Part 1¶

First method-polar coordinate system

Exercise: Plot the ellipse given by the equation \(\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\ \)

1 Use the worksheet (attached at the end).

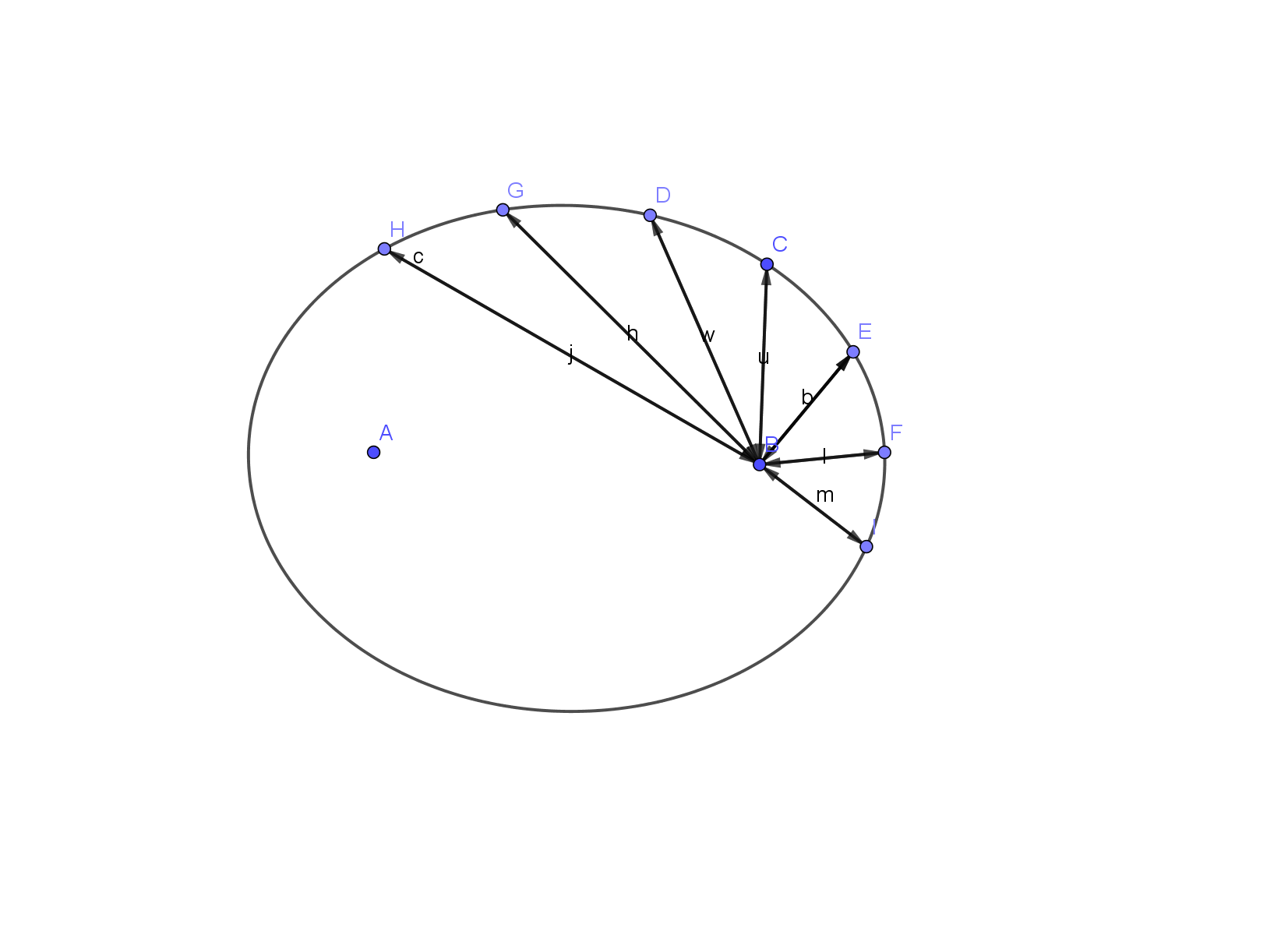
A, B are focals, the path of the robot is marked by vectors. The robot gets to the point e.g. C. Mark point C. And at the point changes direction, the rear wheels become front and the robot goes back to the starting point. The circumference of the wheel is 17,584 but we use 18 cm . Divide r by 18 to get the number of rotations.

Write the programme and use the data from the table. (You can try to prepare your own programme for filling the table).

Advice 1: Our ellipse was 1 meter large. It can be smaller.

Advice 2: Put the robot in the right focus and repeat the programme. You will get more points on the curve.

Advice 3: Use a light dark pen to plot the points

We were pleased with the result. The points were not visible enough, so we had to mark them with the black pencil. The robot made small mistakes. Try also other conic sections!

Second method- physical approach

Exercise. Plot a circle with a given radius.

\(o_{l} = 2\pi r\ \ \ \ o_{r} = 2\pi\left( r + 12 \right)\)

\(v = \frac{s}{t}\text{ }v_{l} = \frac{2\pi \bullet 50}{10}\) , \(v_{r} = \frac{2\pi \bullet 62}{10}\)

Plot an ellipse using velocity.

The parametric equations of the ellipse are \(x = a \bullet cos\ t,\ \ y = b \bullet sin\ t\)

With derivative, we get velocities (4th grade)

\(v_{x} = - a \bullet sint,\ \ v_{y} = b \bullet cost.\)

The total speed on one wheel is

\(v =\sqrt{v_x^2 + v_y^2}\)

We also determine the speed for the outer wheel. The distance between the wheels is 12 cm.

Short help on programming¶

Commands/functions needed for the exercise

Commands necessary to move

#!/usr/bin/env python3

from ev3dev2.motor import MoveTank, OUTPUT_B, OUTPUT_C

tank=MoveTank(OUTPUT_B,OUTPUT_C)

tank.on_for_rotations(20,20,1)

tank.on(-20,20)

tank.off()

Commands necessary to pen

#!/usr/bin/env python3

from ev3dev2.motor import MediumMotor, OUTPUT_D

mm=MediumMotor(OUTPUT_D)

mm.on_for_rotations(5,0.15)

mm.on_for_rotations(-5,0.15)

Worksheet for students

Exercise: Plot the ellipse given by the equation \(\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\)

• a= …, b=…., e=…., p=…..