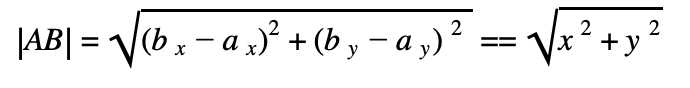Point to point drawing function¶
Preparing For This Tutorial:¶
The LEGO Mindstorm EV3 Robot that coincides with this tutorial comes from building specific sections found in the LEGO Mindstorm Education Core Set building instructions. You should construct the Robot Educator base model, Moreover students should know the Lessons: Basic - Motors, Circle and its application (program presented in this topic is necessary for this lesson),
Related topics: The conic sections
Time constraints:
Starting from 90 min - double lesson
Exercises¶
Create a program to check the value of tan when the measure of angle is equal \(60,\ - 60,\ 120,\ - 120\) degrees.
On piece of paper mark following points\((\sqrt{3},1),\ ( \sqrt{3} ,1),\ (\sqrt{3}, - 1),\ ( -\sqrt{3} \ , - 1)\) in the coordinate system. Create a program to see the difference between functions: atan and atan2. As argument put \(\sqrt{3}\) or \(-\sqrt{3}\) for atan function and\((\sqrt{3}, 1),\ ( - \sqrt{3} ,1),\ (\sqrt{3}, - 1),\ ( -\sqrt{3} \ , - 1)\) for atan2.
Create a program that will cause the robot to move from point (0,0) to any other point in the coordinate system. To check the program result use the following pairs of points [(0.0), (10,10)], [(0.0), (-10,0)], [(0.0), (0,-10)], [(0,0),(-10,-10)] or similar.
Create a program for the robot to plot the function \(y = sin\ x\)or \(y = x{}^{2}\)
Theory¶
Mathematics
In order for the robot to move from point to point in the coordinate system first it turns by a certain angle (see Circle and its applications lesson), next it determines the segment. So we have got two problems:
How to compute the angle the robot should turn around?
How to compute the segment length?
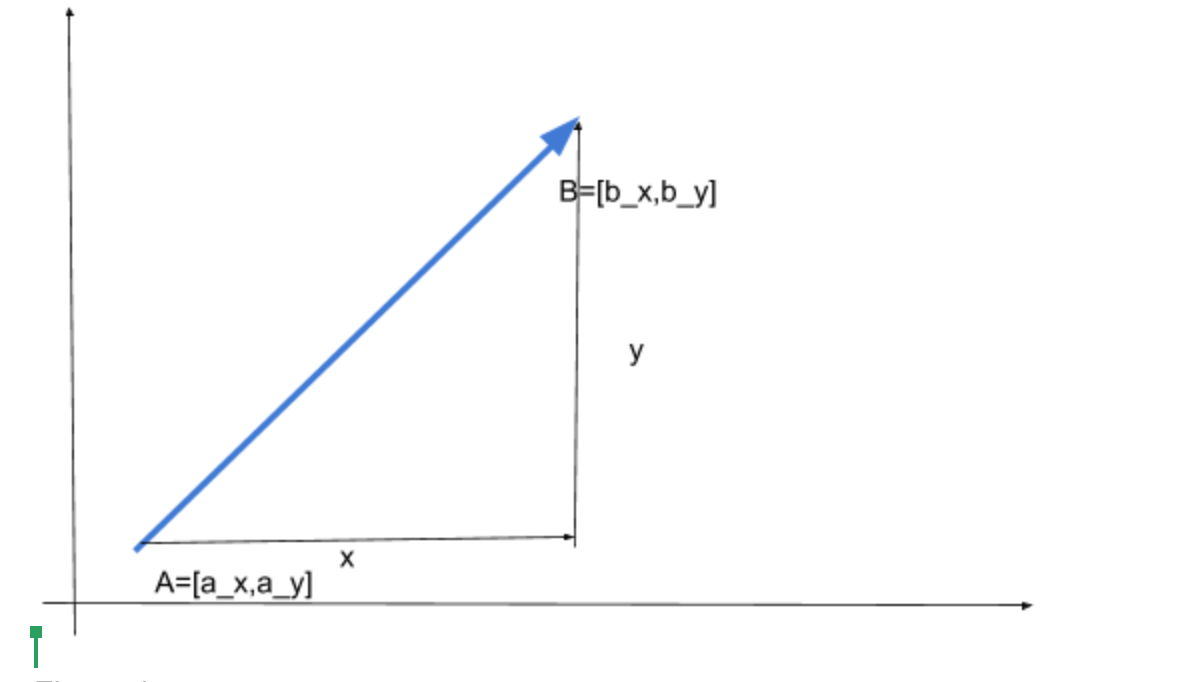
Let investigate the coordinate system and the vector 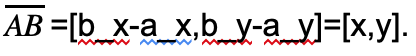
We would like that robot goes from point A to point B.
For solving the second problem we will apply the Pythagorean theorem.
For solving the first problem we’ll apply trigonometric functions.
THE ANGLES in math are in radian measure.
\(180{}^{\circ}\text{ }\pi\text{ radians }\)
\(\text{y }{}^{\circ}\text{ x radians}\)
so we have conversion \(y{}^{\circ} = \frac{180{}^{\circ}\text{ x}}{\pi}\) and \(x\ radians\ = \frac{y{}^{\circ}\pi}{180}\ \)
- According to figure no 1 we can write
\(\text{tan }\alpha\ = \ \frac{y}{\text{x }} = \frac{\left| by_{} - a_{y} \right|}{\left| b_{x} - a_{x} \right|}\).
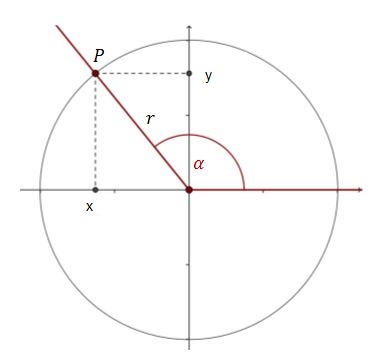
- For extending these definitions for an arbitrary point in the
coordinate system, we can use geometrical definitions using the standard unit circle (a circle with radius 1 unit).
\(\text{tan }\alpha\ = \frac{y}{\text{x }}\ (x \neq 0)\)
Determine the values of the trigonometric functions of the following angles.
\(tan\ (60{}^{0}) = tan\ (\ \frac{\pi}{3})\ = \sqrt{3}\)
\(tan\ ( - 120{}^{0}) = tan\ ( - \frac{2\pi}{3})\ = \ - tan(\pi - \frac{\pi}{3}) = tan(\frac{\pi}{3}) = \sqrt{3}\)
\(tan\ ( - 60{}^{0}) = tan\ (\ \frac{\pi}{- 3})\ = - \sqrt{3}\)
\(tan\ (120{}^{0}) = tan\ (\ \frac{2\pi}{3})\ = \ tan(\pi - \frac{\pi}{3}) = \ - tan(\frac{\pi}{3}) = - \sqrt{3}\)
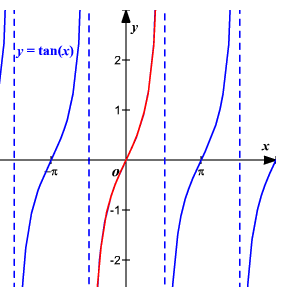
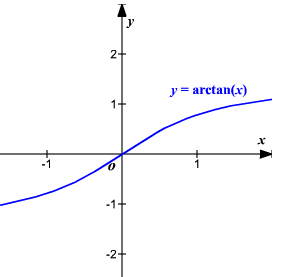
We see that for different angles we obtain the same value. So can we get the angle value when we give the tangent value? Let’s look at the function \(y = tan\ x\ \)plot. We can take the inverse function to \(y = \ tan\ x\)only in the interval \((\frac{- \pi}{2},\frac{\pi}{2})\ \).
The arctangent is the inverse of tangent. Tangent is just a ratio, and arctangent tells what degrees (radians) that angle is. In general, if you know the trig ratio but not the angle, you can use the corresponding inverse trig function to find the angle.
Part 1¶
Computer science
Exercise 1:
Exercise 2:
Use atan2(y,x) python function. Python function atan2(y,x)returns value of \(atan(y/x)\) in radians, value between \(- \pi\) and \(\pi\) representing the angle θ made between the line segment from the origin to P and the positive x-axis.
Exercise 3
Step 1
Step 2 Use the program presented in lesson Circle and its applications. Try this program with R1=0.5R track width. Why will this modification be better for us?
Step 3
Create a program so that the robot move straight by the length of the vector with the given coordinates.
Mathematics
We need to determine the number of rotations of the robot wheels (compare with lesson Circle and its applications).. The distance is equal to the circumference of the robot wheel \((2\pi r = \pi d = 17.58\ \ r\) is a radius of robot’s wheel) multiplied by the number of rotations, so
\(distance\ cm\ = \pi\text{d rotations}\) .
But on the other side the distance is equal (see theory above) \(distance\ = \sqrt{x^2 + y^2}\)
so
\(rotations = \frac{\sqrt{x^2 + y^2}}{\pi d}\)
Modify the function gostright() presented in lesson Circle and its applications.
Step 4
Use the program presented in step 2 and step 3. To obtain the measure of angle use program from exercise 2.
Exercise 4
Mathematics
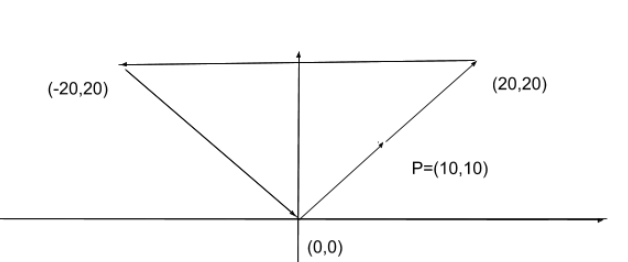
Get the coordinates of two adjacent points. Determine the coordinates of the vector. Move the robot by this vector. Note when determining the rotation angle, update the designated new_ angle with the current position of the robot. Let’s make a test. Mark the points [[0,0],[10,10],[20,20],[-20,20],[0,0]] and compute vectors and angles.
\(A = \lbrack 0,0\rbrack\ ,\ B = \lbrack 10,10\rbrack\ AB = \lbrack 10,10\rbrack\ \alpha = atan(10,10) = 45^{\circ}\)
\(A = \lbrack 10,10\rbrack\ ,\ B = \lbrack 20,20\rbrack\ AB = \lbrack 10,10\rbrack\ \alpha = atan(10,10) = 45^{\circ}\)but rotation is not necessary - use if conditions.
\(A = \lbrack 20,20\rbrack\ ,\ B = \lbrack - 20,20\rbrack\ AB = \lbrack - 40,0\rbrack\ \alpha = atan(0, - 40) = 180^{\circ}\)\(angle = new\_ angle\ = 45\),
\(rotations\ angle = new\_ angle - old\_ anlge = 180^{\circ} - 45^{\circ} = 135^{\circ}\) update angle \(angle = new\_ angle\ = 180\)
\(A = \lbrack - 20,20\rbrack\ ,\ B = \lbrack 0,0\rbrack\ AB = \lbrack 20, - 20\rbrack\ \alpha = atan( - 20,20) = {- 45}^{\circ}\)
\(angle = new\_ angle - old\_ anlge = \ - 45^{\circ} - 180^{\circ} = {- 225}^{\circ}\),
Short help on programming¶
Commands/functions needed for the exercises
math.atan(x)
Returns the arc tangent of x in radians.
math.tan(x)
Returns the tangent of x.
math.atan2(*y*, *x*)
Returns the arc tangent of (y / x) in radians (the same as atan for(y/x)). The result is between -pi and pi. The vector in the plane from the origin to point (x, y) makes this angle with the positive X axis. The point of atan2() is that the signs of both inputs are known to it, so it can compute the correct quadrant for the angle.
math.degrees(*x*)
Convert angle x from radians to degrees. You could prepare your own version of this function.
tank_pair = MoveTank(OUTPUT_B, OUTPUT_C)
Define the motor pair. Before you can use this function you must import it.
on_for_rotations(left_speed, right_speed, rotations, brake=True, block=True)
Rotate the motors at left_speed and right_speed for rotations. Left_speed and right_speed are integer percentages of the rated maximum speed of the motor.