Circle measure the distance¶
Preparing For This Tutorial:¶
- The LEGO Mindstorm EV3 Robot that coincides with this tutorial comes
from building specific sections found in the LEGO Mindstorm Education - Driving Base.
- For the first exercise, you can use a simple model presented below
(measuring Wheel):
Figure no 1 - Measuring Wheel
Time constraints:
starting from 45 min - single lesson
Exercises¶
Create a programme that will display the distance travelled by the wheel (see Figure nr 1). Draw a large infinity symbol on the floor and try to measure it.
Create a programme which will allow you to measure the average velocity of your robot.
Create a programme which will allow you to measure the instantaneous velocity of your robot.
Theory¶
Exercise 1
Measure the circumference of a circle with a thread and compare the results with colleagues in the group.
Calculate the circumference of the circle using the formula \(\text{Circumference}\ = 2 \times \pi \times \text{radius}\)
The distance is therefore equal to the circumference multiplied by the number of rotations.
\(distance\ = \text{Circumference } \times \text{rotations}\ \)
How to count the number of rotations? Use the property position from
class LargeMotor which returns the current position of the motor in
pulses of the rotary encoder. When the motor rotates clockwise, the
position will increase. Likewise, rotating counter-clockwise causes the
position to decrease. We consider the situation when the robot drives
forward (or turns) but does not go backward. We get the number of
rotations by dividing the value of the variable position by 360. Use the
class Button to stop the programme. The programme for begin is presented
below. 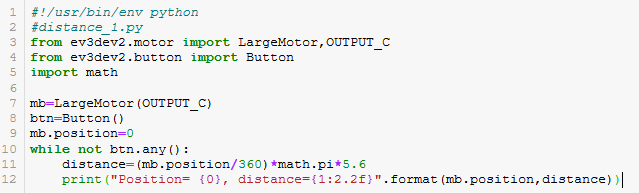
Exercise 2a
Average velocity is defined to be the change in position divided by the time of travel.
\(v{}_{\text{avg }} = \frac{\Delta d}{\Delta t}\).
Modify the above programme to appoint the value of average velocity.
It is obvious that if the vehicle has stopped the average speed will decrease. Modifying the above code makes it possible to observe changes in the average speed. Use the right button from the brick to stop motors and enter button to stop the programme.
Exercise 2b
Step 1
Physics science
How to compute the instantaneous velocity? If we consider v as velocity and d as the displacement (change in position) vector, then we can express the (instantaneous) velocity of a particle or object, at any particular time t, as the derivative of the position with respect to time.
\(v = \lim_{\Delta t \rightarrow 0}\frac{\Delta d}{\Delta t}\).
Computer science
From a programming point of view, we need a small period of time and a short distance related to this time. These values should be updated during each loop around.
Step 2.
Use the arithmetic mean of the left and right motor’s values to get the correct results when the robot turns (try to change the steering value).
Short help on programming¶
Commands/functions needed for the exercise
Import the library
#!/usr/bin/env python3
from ev3dev2.motor import LargeMotor,OUTPUT_B
Create an instance of class
#!/usr/bin/env python3
mb=LargeMotors(OTPUT_B)
The useful property position from LargeMotor class
position
returns the current position of the motor in pulses of the rotary encoder. When the motor rotates clockwise, the position will increase. Likewise, rotating counter-clockwise causes the position to decrease. Writing will set the position to that value.
Example:
#!/usr/bin/env python3
mb.positon
Import the library
#!/usr/bin/env python3
from ev3dev2.button import Button
Create an instance of class
btn=Button()
Function any from class Button
any()
Example:
#!/usr/bin/env python3
while not btn.any():
Other possibilities to end program:
Example:
#!/usr/bin/env python3
while not btn.left
Import the library
#!/usr/bin/env python3
from ev3dev2.motor import MoveSteering
import time
pair the motors
steer_pair=MoveSteering(OUTPUT_C,OUTPUT_B)
function from the MoveSteering class to control two engines together.
on (steer, speed)
Return the time in seconds since the epoch as a floating point number. The specific date of the epoch and the handling of leap seconds is platform dependent. On Windows and most Unix systems, the epoch is January 1, 1970, 00:00:00 (UTC) and leap seconds are not counted towards the time in seconds since the epoch. time()
Example:
#!/usr/bin/env python3
start_t=time.time()
while True:
t=time.time()-start_t